CS50-Ergänzungsmaterialien (Woche 3, Vorlesungen 7 und 8): Asymptotische Notation, Sortier- und Suchalgorithmen

Vorlesungen aus dem Harvard-Kurs zu Programmiergrundlagen CS50 CS50-Aufgaben, Woche 3, Teil 1 CS50-Aufgaben, Woche 3, Teil 2

Asymptotische Notation

Die Geschwindigkeit eines Algorithmus in Echtzeit – in Sekunden und Minuten – zu messen, ist nicht einfach. Ein Programm kann langsamer laufen als ein anderes, nicht aufgrund seiner eigenen Ineffizienz, sondern aufgrund der Langsamkeit des Betriebssystems, der Inkompatibilität mit der Hardware, der Belegung des Computerspeichers durch andere Prozesse ... Um die Wirksamkeit von Algorithmen zu messen, wurden universelle Konzepte erfunden , unabhängig von der Umgebung, in der das Programm ausgeführt wird. Die asymptotische Komplexität eines Problems wird mithilfe der Big-O-Notation gemessen. Seien f(x) und g(x) Funktionen, die in einer bestimmten Umgebung von x0 definiert sind und g dort nicht verschwindet. Dann ist f „O“ größer als g für (x -> x0), wenn es eine Konstante C> gibt 0 , dass für alle x aus einer Umgebung des Punktes x0 die Ungleichung gilt. |f(x)| <= C |g(x)| Etwas weniger streng: f ist „O“ größer als g, wenn es eine Konstante C>0 gibt, die für alle x > x0 gilt. f(x) <= C*g(x) Keine Angst die formale Definition! Im Wesentlichen bestimmt es den asymptotischen Anstieg der Programmlaufzeit, wenn die Menge Ihrer Eingabedaten in Richtung Unendlich wächst. Sie vergleichen beispielsweise die Sortierung eines Arrays mit 1000 Elementen und 10 Elementen und müssen verstehen, wie sich die Laufzeit des Programms verlängert. Oder Sie müssen die Länge einer Zeichenfolge berechnen, indem Sie Zeichen für Zeichen vorgehen und für jedes Zeichen 1 hinzufügen: c - 1 a - 2 t - 3 Seine asymptotische Geschwindigkeit = O(n), wobei n die Anzahl der Buchstaben im Wort ist. Wenn Sie nach diesem Prinzip zählen, ist die Zeit, die zum Zählen der gesamten Zeile benötigt wird, proportional zur Anzahl der Zeichen. Das Zählen der Zeichen in einer Zeichenfolge mit 20 Zeichen dauert doppelt so lange wie das Zählen der Zeichen in einer Zeichenfolge mit zehn Zeichen. Stellen Sie sich vor, dass Sie in der Längenvariablen einen Wert gespeichert haben, der der Anzahl der Zeichen in der Zeichenfolge entspricht. Beispiel: Länge = 1000. Um die Länge einer Zeichenfolge zu ermitteln, benötigen Sie nur Zugriff auf diese Variable; Sie müssen sich nicht einmal die Zeichenfolge selbst ansehen. Und egal wie wir die Länge ändern, wir können immer auf diese Variable zugreifen. In diesem Fall ist die asymptotische Geschwindigkeit = O(1). Eine Änderung der Eingabedaten ändert nichts an der Geschwindigkeit einer solchen Aufgabe; die Suche wird in einer konstanten Zeit abgeschlossen. In diesem Fall ist das Programm asymptotisch konstant. Nachteil: Sie verschwenden Computerspeicher für die Speicherung einer zusätzlichen Variablen und zusätzliche Zeit für die Aktualisierung ihres Werts. Wenn Sie glauben, dass die lineare Zeit schlecht ist, können wir Ihnen versichern, dass es noch viel schlimmer sein kann. Zum Beispiel O(n ² ). Diese Notation bedeutet, dass mit zunehmendem n die Zeit, die zum Durchlaufen von Elementen (oder einer anderen Aktion) erforderlich ist, immer stärker zunimmt. Aber für kleine n können Algorithmen mit der asymptotischen Geschwindigkeit O(n ² ) schneller arbeiten als Algorithmen mit der asymptotischen Geschwindigkeit O(n). Aber irgendwann wird die quadratische Funktion die lineare überholen, daran führt kein Weg vorbei. Eine weitere asymptotische Komplexität ist die logarithmische Zeit oder O(log n). Mit zunehmendem n nimmt diese Funktion sehr langsam zu. O(log n) ist die Laufzeit des klassischen binären Suchalgorithmus in einem sortierten Array (erinnern Sie sich an das zerrissene Telefonbuch in der Vorlesung?). Das Array wird in zwei Teile geteilt, dann wird die Hälfte ausgewählt, in der sich das Element befindet, und so wird jedes Mal, wenn wir den Suchbereich um die Hälfte reduzieren, nach dem Element gesucht. Was passiert, wenn wir sofort auf das Gesuchte stoßen und unser Datenarray zum ersten Mal in zwei Hälften teilen? Es gibt einen Begriff für die beste Zeit – Omega-groß oder Ω(n). Bei binärer Suche = Ω(1) (findet in konstanter Zeit, unabhängig von der Größe des Arrays). Die lineare Suche läuft in der Zeit O(n) und Ω(1), wenn das gesuchte Element das allererste ist. Ein weiteres Symbol ist Theta (Θ(n)). Es wird verwendet, wenn die besten und schlechtesten Optionen gleich sind. Dies eignet sich für ein Beispiel, bei dem wir die Länge eines Strings in einer separaten Variablen gespeichert haben, sodass es für jede Länge ausreicht, auf diese Variable zu verweisen. Für diesen Algorithmus sind der beste und der schlechteste Fall Ω(1) bzw. O(1). Das bedeutet, dass der Algorithmus in der Zeit Θ(1) läuft.

Lineare Suche

Wenn Sie einen Webbrowser öffnen, nach einer Seite, Informationen oder Freunden in sozialen Netzwerken suchen, führen Sie eine Suche durch, genau wie wenn Sie versuchen, in einem Geschäft das richtige Paar Schuhe zu finden. Sie haben wahrscheinlich bemerkt, dass Ordnung einen großen Einfluss auf Ihre Suche hat. Wenn Sie alle Ihre Hemden im Schrank haben, ist es in der Regel einfacher, das benötigte Hemd darunter zu finden, als unter denen, die ohne System im Raum verstreut sind. Die lineare Suche ist eine Methode der sequentiellen Suche nacheinander. Wenn Sie die Google-Suchergebnisse von oben nach unten überprüfen, verwenden Sie eine lineare Suche. Beispiel . Nehmen wir an, wir haben eine Liste mit Zahlen: 2 4 0 5 3 7 8 1 Und wir müssen 0 finden. Wir sehen es sofort, aber ein Computerprogramm funktioniert nicht so. Sie beginnt am Anfang der Liste und sieht die Zahl 2. Dann prüft sie: 2=0? Das ist nicht der Fall, also fährt sie fort und geht zur zweiten Figur über. Auch dort erwartet sie ein Misserfolg, und erst an dritter Stelle findet der Algorithmus die benötigte Zahl. Pseudocode für die lineare Suche: Die linearSearch-Funktion erhält zwei Argumente als Eingabe – den Schlüssel key und das Array array[]. Der Schlüssel ist der gewünschte Wert, im vorherigen Beispiel key = 0. Das Array ist eine Liste von Zahlen, die wir verwenden Werde durchschauen. Wenn wir nichts gefunden haben, gibt die Funktion -1 zurück (eine Position, die im Array nicht existiert). Wenn die lineare Suche das gewünschte Element findet, gibt die Funktion die Position zurück, an der sich das gewünschte Element im Array befindet. Das Gute an der linearen Suche ist, dass sie für jedes Array funktioniert, unabhängig von der Reihenfolge der Elemente: Wir durchsuchen immer noch das gesamte Array. Das ist auch seine Schwäche. Wenn Sie die Zahl 198 in einem Array von 200 der Reihe nach sortierten Zahlen finden müssen, durchläuft die for-Schleife 198 Schritte. Sie haben wahrscheinlich schon erraten, welche Methode für ein sortiertes Array besser funktioniert?

Binäre Suche und Bäume

Stellen Sie sich vor, Sie haben eine alphabetisch sortierte Liste mit Disney-Figuren und müssen Mickey Mouse finden. Linear würde es lange dauern. Und wenn wir die „Methode, das Verzeichnis in zwei Hälften zu zerreißen“ anwenden, gelangen wir direkt zu Jasmine und können die erste Hälfte der Liste getrost verwerfen, da wir erkennen, dass Mickey nicht dort sein kann. Nach dem gleichen Prinzip verwerfen wir die zweite Spalte. Wenn wir diese Strategie fortsetzen, werden wir Mickey in nur wenigen Schritten finden. Suchen wir die Zahl 144. Wir teilen die Liste in zwei Hälften und erhalten die Zahl 13. Wir bewerten, ob die gesuchte Zahl größer oder kleiner als 13 ist. 13 < 144, sodass wir alles links davon ignorieren können 13 und diese Zahl selbst. Jetzt sieht unsere Suchliste so aus: 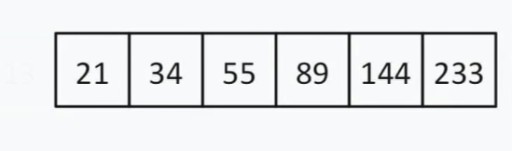Es gibt eine gerade Anzahl von Elementen, also wählen wir das Prinzip, nach dem wir die „Mitte“ (näher am Anfang oder Ende) auswählen. Nehmen wir an, wir haben die Strategie der Nähe zum Anfang gewählt. In diesem Fall ist unsere „Mitte“ = 55. 55 < 144. Wir verwerfen die linke Hälfte der Liste wieder. Zu unserem Glück ist die nächste durchschnittliche Zahl 144. Mit der binären Suche haben wir in nur drei Schritten 144 in einem 13-Elemente-Array gefunden. Eine lineare Suche würde die gleiche Situation in bis zu 12 Schritten bewältigen. Da dieser Algorithmus die Anzahl der Elemente im Array bei jedem Schritt um die Hälfte reduziert, findet er das benötigte Element in der asymptotischen Zeit O(log n), wobei n die Anzahl der Elemente in der Liste ist. Das heißt, in unserem Fall ist die asymptotische Zeit = O(log 13) (das ist etwas mehr als drei). Pseudocode der binären Suchfunktion: 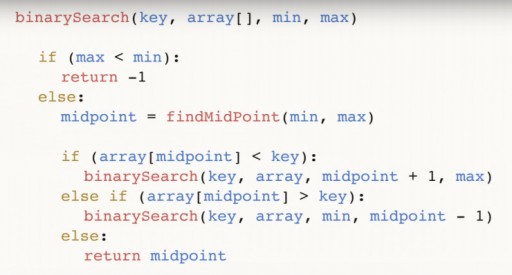Die Funktion benötigt 4 Argumente als Eingabe: den gewünschten Schlüssel, das Datenarray array [], in dem sich das gewünschte befindet, min und max sind Zeiger auf die maximale und minimale Zahl im Array, die Wir betrachten diesen Schritt des Algorithmus. Für unser Beispiel wurde zunächst folgendes Bild gegeben: Analysieren wir den Code weiter. midpoint ist unsere Mitte des Arrays. Es hängt von den Extrempunkten ab und ist zwischen diesen zentriert. Nachdem wir die Mitte gefunden haben, prüfen wir, ob diese kleiner als unsere Schlüsselzahl ist. Wenn ja, dann ist key auch größer als alle Zahlen links von der Mitte, und wir können die Binärfunktion erneut aufrufen, nur dass jetzt min = Mittelpunkt + 1 ist. Wenn sich herausstellt, dass key < Mittelpunkt ist, können wir verwerfen diese Zahl selbst und alle Zahlen, die rechts von ihm liegen. Und wir rufen eine binäre Suche durch das Array von der Zahl min bis zum Wert (Mittelpunkt – 1) auf. Schließlich der dritte Zweig: Wenn der Wert in der Mitte weder größer noch kleiner als der Schlüssel ist, hat er keine andere Wahl, als die gewünschte Zahl zu sein. In diesem Fall geben wir es zurück und beenden das Programm. Schließlich kann es vorkommen, dass die gesuchte Zahl überhaupt nicht im Array enthalten ist. Um diesen Fall zu berücksichtigen, führen wir folgende Prüfung durch: Und wir geben (-1) zurück, um anzuzeigen, dass wir nichts gefunden haben. Sie wissen bereits, dass die binäre Suche eine Sortierung des Arrays erfordert. Wenn wir also ein unsortiertes Array haben, in dem wir ein bestimmtes Element finden müssen, haben wir zwei Möglichkeiten:

1. Sortieren Sie die Liste und wenden Sie die binäre Suche an
2. Sorgen Sie dafür, dass die Liste immer sortiert bleibt, während Sie gleichzeitig Elemente hinzufügen und daraus entfernen.

Eine Möglichkeit, Listen sortiert zu halten, ist die Verwendung eines binären Suchbaums. Ein binärer Suchbaum ist eine Datenstruktur, die die folgenden Anforderungen erfüllt:

• Es ist ein Baum (eine Datenstruktur, die eine Baumstruktur emuliert – sie hat eine Wurzel und andere Knoten (Blätter), die durch „Zweige“ oder Kanten ohne Zyklen verbunden sind)
• Jeder Knoten hat 0, 1 oder 2 Kinder
• Sowohl der linke als auch der rechte Teilbaum sind binäre Suchbäume.
• Alle Knoten des linken Teilbaums eines beliebigen Knotens X haben Datenschlüsselwerte, die kleiner sind als der Wert des Datenschlüssels von Knoten X selbst.
• Alle Knoten im rechten Teilbaum eines beliebigen Knotens X haben Datenschlüsselwerte, die größer oder gleich dem Wert des Datenschlüssels von Knoten X selbst sind.

Achtung: Die Wurzel des „Programmierer“-Baums befindet sich im Gegensatz zum echten Baum oben. Jede Zelle wird als Scheitelpunkt bezeichnet und die Scheitelpunkte sind durch Kanten verbunden. Die Wurzel des Baums ist Zelle Nummer 13. Der linke Teilbaum von Scheitelpunkt 3 ist im Bild unten farblich hervorgehoben: 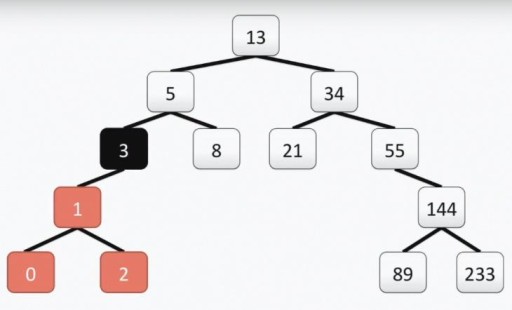Unser Baum erfüllt alle Anforderungen für Binärbäume. Dies bedeutet, dass jeder seiner linken Teilbäume nur Werte enthält, die kleiner oder gleich dem Wert des Scheitelpunkts sind, während der rechte Teilbaum nur Werte enthält, die größer oder gleich dem Wert des Scheitelpunkts sind. Sowohl der linke als auch der rechte Teilbaum sind selbst binäre Teilbäume. Die Methode zur Konstruktion eines Binärbaums ist nicht die einzige: Unten im Bild sehen Sie eine weitere Option für denselben Zahlensatz, und in der Praxis kann es viele davon geben. Diese Struktur hilft bei der Suche: Wir finden den Mindestwert, indem wir uns jedes Mal von oben nach links und nach unten bewegen. 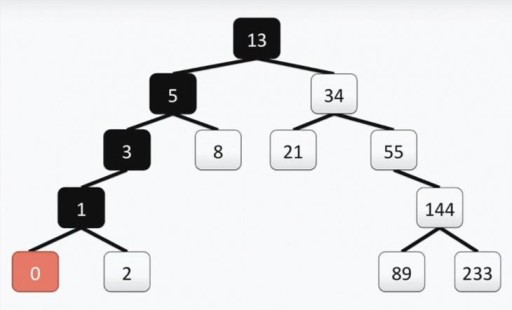Wenn Sie die maximale Anzahl ermitteln müssen, gehen wir von oben nach unten und nach rechts vor. Es ist auch ganz einfach, eine Zahl zu finden, die nicht das Minimum oder Maximum ist. Wir steigen von der Wurzel nach links oder nach rechts ab, je nachdem, ob unser Scheitelpunkt größer oder kleiner als der gesuchte ist. Wenn wir also die Zahl 89 finden müssen, gehen wir diesen Weg: Sie können die Zahlen auch in sortierter Reihenfolge anzeigen. Wenn wir beispielsweise alle Zahlen in aufsteigender Reihenfolge anzeigen müssen, nehmen wir den linken Teilbaum und gehen vom Scheitelpunkt ganz links nach oben. Auch das Hinzufügen von etwas zum Baum ist einfach. Das Wichtigste, woran man sich erinnern sollte, ist die Struktur. Nehmen wir an, wir müssen dem Baum den Wert 7 hinzufügen. Gehen wir zur Wurzel und überprüfen dies. Die Zahl 7 < 13, also gehen wir nach links. Wir sehen dort 5 und gehen nach rechts, da 7 > 5. Da 7 > 8 und 8 keine Nachkommen hat, konstruieren wir außerdem einen Zweig von 8 nach links und hängen 7 daran an. Sie können auch Scheitelpunkte entfernen der Baum, aber das ist etwas komplizierter. Es gibt drei verschiedene Löschszenarien, die wir berücksichtigen müssen.

1. Die einfachste Option: Wir müssen einen Scheitelpunkt löschen, der keine untergeordneten Elemente hat. Zum Beispiel die Zahl 7, die wir gerade hinzugefügt haben. In diesem Fall folgen wir einfach dem Pfad zum Scheitelpunkt mit dieser Nummer und löschen ihn.
2. Ein Scheitelpunkt hat einen untergeordneten Scheitelpunkt. In diesem Fall können Sie den gewünschten Scheitelpunkt löschen, aber sein Nachkomme muss mit dem „Großvater“ verbunden sein, also dem Scheitelpunkt, aus dem sein unmittelbarer Vorfahre hervorgegangen ist. Zum Beispiel müssen wir aus demselben Baum die Zahl 3 entfernen. In diesem Fall verbinden wir seinen Nachkommen, eins, zusammen mit dem gesamten Unterbaum zu 5. Dies geschieht einfach, da alle Scheitelpunkte links von 5 sein werden weniger als diese Zahl (und weniger als das entfernte Dreifache).
3. Der schwierigste Fall ist, wenn der zu löschende Scheitelpunkt zwei untergeordnete Elemente hat. Jetzt müssen wir als erstes den Scheitelpunkt finden, in dem der nächstgrößere Wert versteckt ist, wir müssen sie vertauschen und dann den gewünschten Scheitelpunkt löschen. Beachten Sie, dass der Scheitelpunkt mit dem nächsthöheren Wert keine zwei untergeordneten Elemente haben kann. Dann ist sein linkes untergeordnetes Element der beste Kandidat für den nächsten Wert. Entfernen wir den Wurzelknoten 13 aus unserem Baum. Zuerst suchen wir nach der Zahl, die 13 am nächsten kommt, also größer ist. Das ist 21. Vertauschen Sie 21 und 13 und löschen Sie 13.

Es gibt verschiedene Möglichkeiten, Binärbäume zu erstellen, einige davon sind gut, andere nicht so gut. Was passiert, wenn wir versuchen, einen Binärbaum aus einer sortierten Liste zu erstellen? Alle Zahlen werden einfach zum rechten Zweig der vorherigen hinzugefügt. Wenn wir eine Zahl finden wollen, bleibt uns nichts anderes übrig, als einfach der Kette nach unten zu folgen. Es ist nicht besser als die lineare Suche. Es gibt andere Datenstrukturen, die komplexer sind. Aber wir werden sie vorerst nicht berücksichtigen. Sagen wir einfach, dass Sie die Eingabedaten zufällig mischen können, um das Problem der Erstellung eines Baums aus einer sortierten Liste zu lösen.

Sortieralgorithmen

Es gibt eine Reihe von Zahlen. Wir müssen es sortieren. Der Einfachheit halber gehen wir davon aus, dass wir die ganzen Zahlen in aufsteigender Reihenfolge (vom kleinsten zum größten) sortieren. Es gibt mehrere bekannte Möglichkeiten, diesen Prozess durchzuführen. Außerdem können Sie sich jederzeit ein Thema ausdenken und eine Modifikation des Algorithmus entwickeln.

Sortierung nach Auswahl

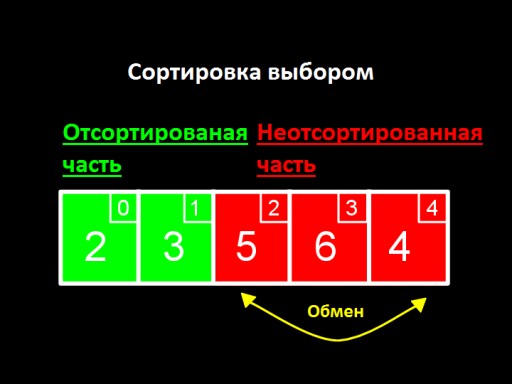Die Hauptidee besteht darin, unsere Liste in zwei Teile aufzuteilen, sortiert und unsortiert. Bei jedem Schritt des Algorithmus wird eine neue Zahl vom unsortierten Teil in den sortierten Teil verschoben und so weiter, bis sich alle Zahlen im sortierten Teil befinden.

1. Finden Sie den minimalen unsortierten Wert.
2. Wir tauschen diesen Wert mit dem ersten unsortierten Wert aus und platzieren ihn so am Ende des sortierten Arrays.
3. Wenn noch unsortierte Werte übrig sind, kehren Sie zu Schritt 1 zurück.

Im ersten Schritt werden alle Werte unsortiert. Nennen wir den unsortierten Teil „Unsorted“ und den sortierten Teil „Sorted“ (das sind nur englische Wörter, und wir machen das nur, weil „Sorted“ viel kürzer ist als „Sorted part“ und auf Bildern besser aussieht). Wir finden die Mindestanzahl im unsortierten Teil des Arrays (d. h. in diesem Schritt im gesamten Array). Diese Zahl ist 2. Jetzt ersetzen wir sie durch die erste der unsortierten und platzieren sie am Ende des sortierten Arrays (in diesem Schritt an erster Stelle). In diesem Schritt ist dies die erste Zahl im Array, also 3. Schritt zwei. Wir schauen uns die Nummer 2 nicht an; sie befindet sich bereits im sortierten Subarray. Wir beginnen mit der Suche nach dem Minimum, beginnend mit dem zweiten Element, das ist 5. Wir stellen sicher, dass 3 das Minimum unter den Unsortierten ist, 5 das erste unter den Unsortierten. Wir tauschen sie aus und fügen 3 zum sortierten Subarray hinzu. Im dritten Schritt sehen wir, dass die kleinste Zahl im unsortierten Subarray 4 ist. Wir ersetzen sie durch die erste Zahl unter den unsortierten – 5. Im vierten Schritt stellen wir fest, dass im unsortierten Array die kleinste Zahl 5 ist. Wir ändern es von 6 und fügen es dem sortierten Subarray hinzu. 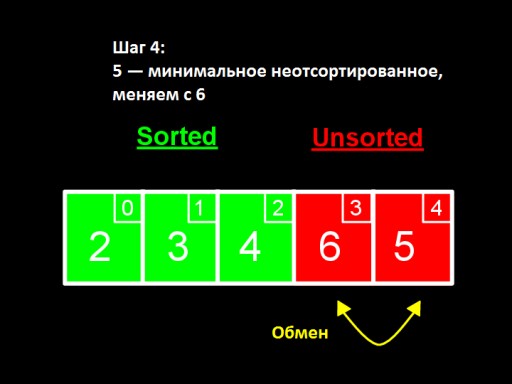Wenn unter den unsortierten nur noch eine Zahl (die größte) übrig bleibt, bedeutet dies, dass das gesamte Array sortiert ist! 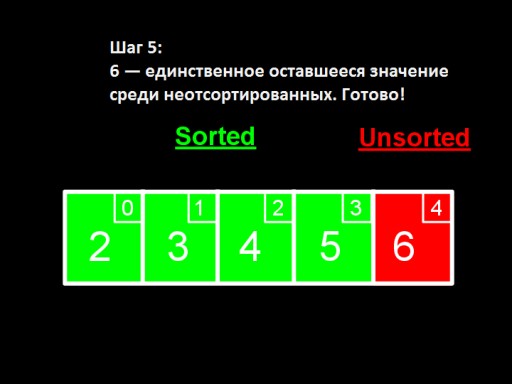So sieht die Array-Implementierung im Code aus. Versuchen Sie es selbst zu machen. Um das minimale unsortierte Element zu finden, müssen wir sowohl im besten als auch im schlechtesten Fall jedes Element mit jedem Element des unsortierten Arrays vergleichen, und wir werden dies bei jeder Iteration tun. Wir müssen jedoch nicht die gesamte Liste anzeigen, sondern nur den unsortierten Teil. Ändert sich dadurch die Geschwindigkeit des Algorithmus? Im ersten Schritt führen wir für ein Array mit 5 Elementen 4 Vergleiche durch, im zweiten 3 und im dritten 2. Um die Anzahl der Vergleiche zu erhalten, müssen wir alle diese Zahlen addieren. Wir erhalten die Summe. Somit beträgt die erwartete Geschwindigkeit des Algorithmus im besten und schlechtesten Fall Θ(n ² ). Nicht der effizienteste Algorithmus! Für Bildungszwecke und für kleine Datensätze ist es jedoch durchaus anwendbar.

Blasensortierung

Der Blasensortierungsalgorithmus ist einer der einfachsten. Wir gehen das gesamte Array entlang und vergleichen zwei benachbarte Elemente. Wenn sie in der falschen Reihenfolge sind, tauschen wir sie aus. Beim ersten Durchgang erscheint das kleinste Element („float“) am Ende (wenn wir in absteigender Reihenfolge sortieren). Wiederholen Sie den ersten Schritt, wenn im vorherigen Schritt mindestens ein Austausch durchgeführt wurde. Sortieren wir das Array. Schritt 1: Gehen Sie das Array durch. Der Algorithmus beginnt mit den ersten beiden Elementen 8 und 6 und prüft, ob sie in der richtigen Reihenfolge sind. 8 > 6, also tauschen wir sie aus. Als nächstes schauen wir uns das zweite und dritte Element an, das sind nun 8 und 4. Aus den gleichen Gründen vertauschen wir sie. Zum dritten Mal vergleichen wir 8 und 2. Insgesamt führen wir drei Austausche durch (8, 6), (8, 4), (8, 2). Der Wert 8 „schwebte“ an der richtigen Position an das Ende der Liste. Schritt 2: Tauschen Sie (6,4) und (6,2). 6 befindet sich nun an vorletzter Stelle und es ist nicht erforderlich, sie mit dem bereits sortierten „Ende“ der Liste zu vergleichen. Schritt 3: Tauschen Sie 4 und 2. Die Vier „schwebt“ an ihren richtigen Platz. Schritt 4: Wir gehen das Array durch, aber wir haben nichts zu ändern. Dies signalisiert, dass das Array vollständig sortiert ist. 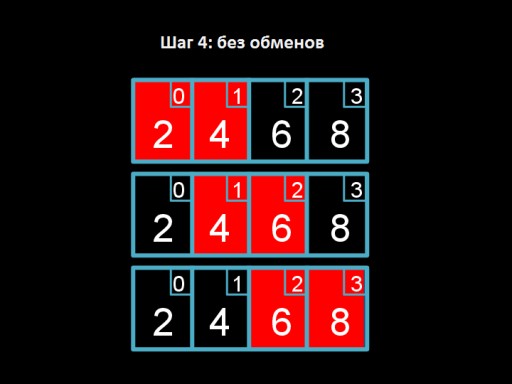Und das ist der Algorithmuscode. Versuchen Sie es in C zu implementieren! Die Blasensortierung dauert im schlimmsten Fall O(n ^{2 ) Zeit (alle Zahlen sind falsch), da wir bei jeder Iteration n Schritte ausführen müssen, von denen es auch n gibt.} Tatsächlich wird die Zeit, wie im Fall des Auswahlsortierungsalgorithmus, etwas kürzer sein (n ² /2 – n/2), aber dies kann vernachlässigt werden. Im besten Fall (wenn alle Elemente bereits vorhanden sind) können wir dies in n Schritten tun, d. h. Ω(n), da wir das Array nur einmal durchlaufen und sicherstellen müssen, dass alle Elemente vorhanden sind (d. h. sogar n-1 Elemente).

Sortieren durch Einfügen

Die Hauptidee dieses Algorithmus besteht darin, unser Array in zwei Teile zu unterteilen, sortiert und unsortiert. Bei jedem Schritt des Algorithmus bewegt sich die Zahl vom unsortierten zum sortierten Teil. Sehen wir uns anhand des folgenden Beispiels an, wie die Einfügungssortierung funktioniert. Bevor wir beginnen, werden alle Elemente als unsortiert betrachtet. Schritt 1: Nehmen Sie den ersten unsortierten Wert (3) und fügen Sie ihn in das sortierte Subarray ein. In diesem Schritt werden das gesamte sortierte Subarray, sein Anfang und sein Ende genau diese drei sein. Schritt 2: Da 3 > 5 ist, fügen wir 5 in das sortierte Unterarray rechts von 3 ein. Schritt 3: Jetzt arbeiten wir daran, die Zahl 2 in unser sortiertes Array einzufügen. Wir vergleichen 2 mit Werten von rechts nach links, um die richtige Position zu finden. Da 2 < 5 und 2 < 3 und wir den Anfang des sortierten Subarrays erreicht haben. Deshalb müssen wir 2 links von 3 einfügen. Dazu verschieben wir 3 und 5 nach rechts, sodass Platz für die 2 ist, und fügen sie am Anfang des Arrays ein. Schritt 4. Wir haben Glück: 6 > 5, also können wir diese Zahl direkt nach der Zahl 5 einfügen. Schritt 5. 4 < 6 und 4 < 5, aber 4 > 3. Daher wissen wir, dass 4 eingefügt werden muss rechts von 3. Wieder sind wir gezwungen, 5 und 6 nach rechts zu verschieben, um eine Lücke für 4 zu schaffen. Fertig! Verallgemeinerter Algorithmus: Nehmen Sie jedes unsortierte Element von n und vergleichen Sie es von rechts nach links mit den Werten im sortierten Subarray, bis wir eine geeignete Position für n finden (d. h. in dem Moment, in dem wir die erste Zahl finden, die kleiner als n ist). . Dann verschieben wir alle sortierten Elemente, die sich rechts von dieser Zahl befinden, nach rechts, um Platz für unser n zu schaffen, und fügen es dort ein, wodurch der sortierte Teil des Arrays erweitert wird. Für jedes unsortierte Element n benötigen Sie:

2. Bestimmen Sie die Position im sortierten Teil des Arrays, an der n eingefügt werden soll
3. Verschieben Sie sortierte Elemente nach rechts, um eine Lücke für n zu schaffen
4. Fügen Sie n in die resultierende Lücke im sortierten Teil des Arrays ein.

Und hier ist der Code! Wir empfehlen, eine eigene Version des Sortierprogramms zu schreiben.

Asymptotische Geschwindigkeit des Algorithmus

Im schlimmsten Fall machen wir einen Vergleich mit dem zweiten Element, zwei Vergleiche mit dem dritten und so weiter. Somit ist unsere Geschwindigkeit O(n ² ). Im besten Fall arbeiten wir mit einem bereits sortierten Array. Der sortierte Teil, den wir von links nach rechts ohne Einfügungen und Bewegungen von Elementen aufbauen, benötigt Zeit Ω(n).

Zusammenführen, sortieren

Dieser Algorithmus ist rekursiv; er zerlegt ein großes Sortierproblem in Teilaufgaben, deren Ausführung es der Lösung des ursprünglichen großen Problems näher bringt. Die Grundidee besteht darin, ein unsortiertes Array in zwei Teile aufzuteilen und die einzelnen Hälften rekursiv zu sortieren. Nehmen wir an, wir müssen n Elemente sortieren. Wenn n < 2, beenden wir die Sortierung, andernfalls sortieren wir den linken und rechten Teil des Arrays getrennt und kombinieren sie dann. Sortieren wir das Array. Teilen Sie es in zwei Teile und teilen Sie es weiter, bis wir Unterarrays der Größe 1 erhalten, die offensichtlich sortiert sind. Zwei sortierte Subarrays können mit einem einfachen Algorithmus in O(n)-Zeit zusammengeführt werden: Entfernen Sie die kleinere Zahl am Anfang jedes Subarrays und fügen Sie sie in das zusammengeführte Array ein. Wiederholen, bis alle Elemente verschwunden sind. Die Zusammenführungssortierung benötigt in allen Fällen O(nlog n) Zeit. Während wir die Arrays auf jeder Rekursionsebene in Hälften teilen, erhalten wir log n. Dann erfordert das Zusammenführen der Subarrays nur n Vergleiche. Daher O(nlog n). Die besten und schlechtesten Fälle für die Zusammenführungssortierung sind gleich, die erwartete Laufzeit des Algorithmus = Θ(nlog n). Dieser Algorithmus ist der effektivste unter den betrachteten.