- Logical operators in Java
- The logical negation operator !
- Logical AND - &, as well as conditional AND - &&
- Logical OR - operator |, as well as conditional OR - operator ||
- XOR - logical exclusive OR - operator ^
- Precedence of logical operations
- Complex Boolean Expressions
- Bitwise (bitwise) operators
- Bitwise operators &, | and ^
- Additional code
- Bitwise negation operator ~

Boolean operations in Java
Logical operations are performed using logical operators. Forgive the tautology, but that's how things are. Basic logical operations (in programming and mathematics) can be applied to logical arguments (operands), as well as more complex expressions, like arithmetic operations on numbers. For example the expression:
(a | b) | (c < 100) & !(true) ^ (q == 5)(a | b), where аand bare type variables boolean (c < 100) (true) (q == 5) In turn, a simple logical expression (a | b)also consists of two operand arguments. A boolean operand is an expression that can be said to be true or false, true or false . In Java language, a boolean operand is an expression of type booleanor Boolean, for example:
(2 < 1)- logical operand, its value is falsetrueis a boolean operand whose value is obviously trueboolean a- can also be a logical operand, like Boolean aint a = 2- is not a logical operand , it is just a variable of typeintString a = "true"is also not a boolean operand . This is a string whose text value is"true".
- Logical negation , it is the same
NOTor inversion. In Java, it is denoted by the character “!” in front of the operand. Applies to one operand. - Logical and , it is
ANDor conjunction. Indicated by the symbol “&” between the two operands to which it applies. - Boolean or in Java , it is -
OR, it is also a disjunction. In Java, denoted by the symbol “|” between two operands. - Exclusive or ,
XOR, strict disjunction. In Java, denoted by the symbol “^” between two operands. - In Java, logical operators include the conditional or , denoted as
||, as well as the conditional and -&&.
==is not commonly referred to as boolean. Attention! In Java, the logical operators&, ,|and^apply to integers as well. In this case, they work a little differently and are called bitwise (or bitwise) logical operators. About them - towards the end of the article. Let's look at a table with a brief description of each of the Java logical operators, and below we will describe them in more detail and give code examples.
| Java operator | Name | Type | Short description | Example |
|---|---|---|---|---|
! |
Logical "not" (negation) | unary | !xmeans "not x". Returns true if the operand is false . Returns false if the operand is true . |
boolean x = true;Then // !x == false |
& |
Logical AND ( AND, multiplication) |
Binary | Returns true if both operands are true . | a = true;b = false;Then a & b == false |
| |
Logical OR ( OR, addition) |
Binary | Returns true if at least one of the operands is true . | a = true;b = false;Then a | b == true |
^ |
Logical XOR ( XOR) |
Binary | Returns true if one and only one of the operands is true . Returns false if both operands are true or false . Essentially returns true if the operands are different. | a = true;b = false;Then a ^ b == true |
&& |
Conditional AND (abbreviated logical AND) | Binary | Same as but &if the operand to the left of &is false , this operator returns false without checking the second operand. |
|
|| |
Conditional OR (abbreviated logical OR) | Binary | Same as but |if the operator on the left is true , the operator returns true without checking the second operand. |
The logical negation operator !
This operator is unary, meaning it applies to a single Boolean expression or operand. It is very simple to understand it, like any negation: the operator simply changes the value of the expression to the opposite. The truth table or the results of the negation operation:| Value a | !a |
| false | true |
| true | false |
public class Solution {
public static void main(String[] args) {
boolean a = true;
System.out.println(!a); // here our boolean expression reverses its value
System.out.println(!false); // non-false expression, as you might guess, will be equal to... what?
System.out.println(!(2 < 5)); // expression (2 < 5) is true, so its negation is false
}
}
false
true
falseLogical AND - &, as well as conditional AND - &&
A logical AND or conjunction is applied to two expressions, and the result of its operation will be true ( true ) only if both operands are true. That is, if one of theaor operands bis false , then the expression a & bwill be false regardless of the value of the second operator. If you imagine that true is the number 1 and false is 0, then the operator &works exactly the same as a normal multiplication. Therefore, logical AND is often called “logical multiplication”. And, by the way, this fact helps to quickly remember the operation of the operator &and not to confuse it with the logical or operator |. Truth table AND, it is also the result of the work of the operator&
| a | b | a&b |
| true | true | true |
| true | false | false |
| false | true | false |
| false | false | false |
public class Solution {
public static void main(String[] args) {
boolean a = true;
boolean b = false;
boolean c = true;
System.out.println(a & b); // if we multiply true by false, we will definitely get false
System.out.println(a & c); // true to true will be true
System.out.println(false & (2 > 5));
System.out.println((2 < 5) & false);
// regardless of the truthfulness of the expression in brackets, in which case we have to be content with false
}
}
false
true
false
false&&is sometimes referred to as the "abbreviated AND". It produces the same result when working with logical operands as the operator &. However, there is a difference in his work itself. So, you have already noticed that if in the expression ( a & b) the operand ais equal to false , then it makes no sense to check the value of the operand b: the result of the operation will definitely be false . So if we do not fundamentally need the value of the second operand, with the help &&we reduce the number of calculations in the program. If we replace all operators in the example &with&&, the result of the work will be exactly the same, but the program itself will run a little faster (although we will not notice this, since we are talking about mi-micro ... in short, about very small units of time).
Logical OR - operator |, as well as conditional OR - operator ||
The OR operator in Java is denoted by the symbol|. A logical OR or disjunction is applied to two expressions, and the result of its operation will be false ( false ) if and only if both operands are false. Here, to some extent, we observe the same picture as in the case of the operator &, but exactly the opposite. That is, if at least one operand is true , then the expression a | bis guaranteed to be true regardless of the value of the second operator. If &it behaves like a logical multiplication, then OR is a logical addition, if you imagine that true is 1 and false- 0. Just remember that logical addition does not work like normal addition. 1 + 1 in this case is not equal to 2, but 1 (the number 2 simply does not exist in this system). Sometimes disjunction is understood as the maximum of 0 and 1, and in this case, if at least one operand is equal to 1 ( true ), we get exactly true . The truth table OR, it is also the result of the operation of the operator |:
| a | b | a | b |
| true | true | true |
| true | false | true |
| false | true | true |
| false | false | false |
public class Solution {
public static void main(String[] args) {
boolean a = true;
boolean b = false;
boolean c = true;
System.out.println(!a | b); // Compose the use of two logical operators: a == true, so !a, as we already know, is false.
System.out.println(a | c);
System.out.println((2 < 5) | false); // expression (2 < 5) is true, which means that for any second operand we get a true result
System.out.println((2 > 5) | true);
}
}
false
true
true
true||instead of |, we will get exactly the same result, but, as in the case of conditional AND &&, it will act sparingly: if we “run into” the first operand equal to true , the value of the second operand is not checked, but immediately the result is true .
XOR Java - Boolean XOR - Operator ^
XOR, modulo 2 addition, logical XOR, logical subtraction, strict disjunction, bitwise complement… the operator ^has many names in boolean algebra. The result of applying this operator to two operands will be true if the operands are different and false if the operands are the same. Therefore, it is convenient to compare it with the subtraction of zeros ( false ) and ones ( true ). Truth table XOR, it is also the result of the operation of the operator ^:
| Boolean a | Boolean b | a^b |
| true | true | false |
| true | false | true |
| false | true | true |
| false | false | false |
public class Solution {
public static void main(String[] args) {
boolean a = true;
boolean b = false;
boolean c = true;
System.out.println(!a ^ b); // Compose the use of two logical operators: a == true, so !a, as we already know, is false.
System.out.println(a ^ c);
System.out.println((2 < 5) ^ false);
System.out.println((2 > 5) ^ true);
}
}
false
false
true
truePrecedence of logical operations
As in mathematics, in programming, operators have a certain order of execution if they occur in the same expression. Unary operators have advantages over binary ones, and multiplication (even logical) over addition. We have arranged logical operators in the list of topics higher, the higher their precedence:!&^|&&||
&and |) have different precedence:
public class Solution {
public static void main(String[] args) {
boolean a = true, b = true, c = false;
System.out.println(a | b & c);
}|and then - &, we would get the value false . But in fact, if you run this program, then make sure that the output is true , because the logical AND operator &will have higher precedence than the logical OR operator |. In order not to get confused, you need to remember that &it behaves like a multiplication, but |like an addition. You can change the order of priority. Just use parentheses, just like in high school math. Let's change our example code a bit:
public class Solution {
public static void main(String[] args) {
boolean a = true, b = true, c = false;
System.out.println((a|b)&c);
}Complex Boolean Expressions
Of course, we can combine logical expressions and operators. Recall the expression from the beginning of the article:(a | b) | (c < 100) & !(true) ^ (q == 5)a, b, сand q. An example of calculating the value of a complex logical expression
public class Solution {
public static void main(String[] args) {
boolean a = true;
boolean b = false;
int c = 25;
int q = 2;
System.out.println((a|b) | (c < 100) & !(true)^(q == 5));
}
}qwe have a variable of type int, but this q == 5is a Boolean expression, and it is equal to false , since we initialized it with qthe number 2 above. The same is with the variable c. This number is 25, but (c < 100) is a boolean expression that evaluates to true . The output of this program:
trueBitwise (bitwise) operators
At the beginning of the article, we mentioned that the&, |and operators ^can be used with Java integer types. In this case, they are bitwise operators. They are also called bitwise, because one bit is one bit, and these operations operate on bits. Of course, they work a little differently than logical operators, and in order to understand exactly how, you need to know what a binary (binary) number system is. If you do not know anything about it or have completely forgotten, we suggest that you first read the article Java: bits and bytes, and we remind everyone else that in the binary number system there are only two digits - 0 and 1, and all data in the computer is represented precisely with the help of conditional zeros and ones. Any of the numbers familiar to us (decimal; for them there are 10 different digits from 0 to 9, with which we write any numbers) is representable in the binary number system. You can convert a decimal number to binary using sequential division into a column on the basis of the number system (2). The remainder of the division at each step, written in reverse order, will give us the binary number we are looking for. Here, for example, is the translation of the decimal number 103 into binary representation: 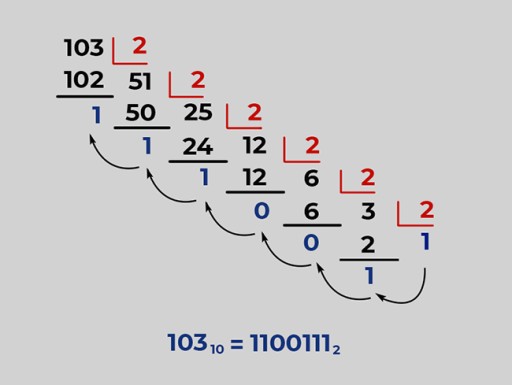
|
Binary number system in CodeGym course In the CodeGym course, they talk about the binary number system while studying the MultiThreading quest (level 10, 1 lecture), after the lecture there are several tasks for fixing. However, this topic is not difficult at all, and even if you have not yet gone through the course that far, most likely you will understand it. |
&, |and ^Java also uses bitwise operators:
~bitwise negation operator>>bit shift right>>>unsigned bitwise right shift<<bitwise left shift
Bitwise operators &, | and ^
Let's look at an example of how these operators work. Let's say we have two integers:int a = 25;
int b = 112; &, |and ^and display the result. Here is the program code:
public class Solution {
public static void main(String[] args) {
int a = 25;
int b = 112;
int res1 = a & b;
int res2 = a | b;
int res3 = a ^ b;
System.out.println("a & b = " + res1);
System.out.println("a | b = " + res2);
System.out.println("a ^ b = " + res3);
}
}
a & b = 16
a | b = 121
a ^ b = 105&, |or ^to the corresponding bits (bits) of both numbers. So, for &the last bit of the binary representation of the number 25, it logically adds up with the last bit of the binary representation of the number 112, the penultimate bit with the penultimate one, and so on:  The same logic can be traced in the case of
The same logic can be traced in the case of |and ^. 
Bit shift left or right
There are several bitwise shift operators in Java. The most commonly used operators<<are and >>. They shift the binary representation of a number to the left or right, respectively, and in the case of a shift to the right, the sign is preserved (what sign preservation means, we will describe below). There is another right shift operator >>>. It does the same as but >>does not save the sign. So, let's look at their work with an example. int a = 13 a << 1shifts all bits of the binary representation of a to the left by 1 bit. To simplify, let's represent the number 13 in binary form as 0000 1101. In fact, this number looks like this:intJava allocates 4 bytes or 32 bits. However, this does not play a role in the example, so in this example we will think our number is one-byte. 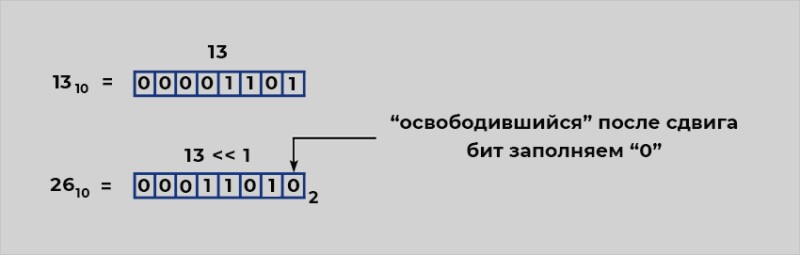 The freed bit on the right is filled with zeros. As a result of such an operation, we get the number 26.
The freed bit on the right is filled with zeros. As a result of such an operation, we get the number 26. a << 2shifts all the bits of the binary representation of the number ato the left by 2 bits, and the two bits freed on the right are filled with zeros. As a result, we will get the number 52. a << 3It will give the result 104 ... Have you noticed a pattern? A bitwise left shift aby n positions works like multiplying a number aby 2 to the power of n. The same goes for negative numbers. This -13 << 3will give the result -104. a >> nshifts the binary representation of a number n places to the right. For example, 13 >> 1 Turns the number 1101 into the number 0110, that is, 6. A13 >> 2will give 3 as a result. That is, in fact, here we divide the number by 2 to the power of n, where n is the number of shifts to the right, but with one nuance: if the number is odd, we kind of reset the last bit of the number during this operation. But with the negative, the situation is somewhat different. Let's say try to check what the program will produce if you ask it to perform the operation -13 >> 1. You will see the number -7, not -6 as you might think. This is due to the nature of storing negative numbers in Java and other programming languages. They are stored in the so-called additional code. In this case, the most significant digit (the one on the left) is given under the sign. In the case of a negative number, the most significant digit is 1.
Additional code
Let's consider a numberint a = 13. If in the program you output its binary representation to the console using the command System.out.println(Integer.toBinaryString(a));, then we will get 1101. In fact, this is an abbreviation, since the number of the type inttakes 4 bytes in memory, so the computer “sees” it, rather like this:
00000000 00000000 00000000 00001101-
We write the number -13 in the so-called “direct code”. To do this, change the most significant digit of the number to 1.
The result of the action:10000000 0000000 0000000 00001101 -
Next, we invert all bits (change 0 to 1, and 1 to 0) except for the sign bit. In fact, we have already changed it.
Action result:11111111 11111111 11111111 11110010(yes, steps 1 and 2 could be combined, but it's better to represent it that way)
- We add 1 to the resulting number.
The result of the action:11111111 11111111 11111111 11110011
-13 >> 1. Since our operator >>is sign-preserving, in this operation, all the bits freed on the left are filled not with zeros, but with ones. Thus shifting the number
11111111 11111111 11111111 11110011
11111111 11111111 11111111 11111001
10000000 00000000 00000000 00000111>>>. a >>> n- this operation is an unsigned shift, that is, it shifts the binary representation of a number ato the right by n bits, but fills the n bits that are freed on the left not with ones, like the operator >>, but with zeros. Let's do the operation -13 >>> 1. We already have a number -13in two's complement:
11111111 11111111 11111111 11110011
01111111 11111111 11111111 111110012147483641.
Bitwise negation operator ~
This unary operator works very simply: it reverses every bit of the binary representation of an integer. Let's take a number-13:
11111111 11111111 11111111 11110011~13will simply reverse the value of each bit. As a result, we will get:
00000000 00000000 00000000 0000110012in decimal.
Brief conclusions
- All logical operators apply to boolean expressions, that is, expressions that can be said to be true or false .
- If the operators
&,|or^are applied to numbers, we are no longer talking about logical operations, but about bitwise ones. That is, both numbers are converted to the binary system and the operations of logical addition, multiplication or subtraction are applied to these numbers bit by bit. - In mathematical logic, the operators
&and|correspond to conjunction and disjunction. - Logical AND is like multiplying 1 ( true ) and 0 ( false ).
- Logical OR is like finding the maximum between 1 ( true ) and 0 ( false ).
- To bitwise negate an integer a, the operation is used
~a. - The operation is used to logically negate the Boolean expression a
!a. - Negative numbers are stored and processed in two's complement.
- A bitwise right shift may
>>or may not preserve the sign (>>>).



GO TO FULL VERSION