Mesurer la vitesse d’un algorithme en temps réel (en secondes et en minutes) n’est pas chose aisée. Un programme peut s'exécuter plus lentement qu'un autre non pas à cause de sa propre inefficacité, mais à cause de la lenteur du système d'exploitation, d'une incompatibilité avec le matériel, de la mémoire de l'ordinateur occupée par d'autres processus... Pour mesurer l'efficacité des algorithmes, des concepts universels ont été inventés. , quel que soit l'environnement dans lequel le programme s'exécute. La complexité asymptotique d'un problème est mesurée à l'aide de la notation Big O. Soit f(x) et g(x) des fonctions définies dans un certain voisinage de x0, et g n'y disparaît pas. Alors f est « O » supérieur à g pour (x -> x0) s'il existe une constante C> 0 , que pour tout x à partir d'un certain voisinage du point x0 l'inégalité est vraie. |f(x)| <= C |g(x)| Légèrement moins stricte : f est « O » supérieur à g s'il existe une constante C>0, qui pour tout x > x0 f(x) <= C*g(x) N'ayez pas peur la définition formelle ! Essentiellement, il détermine l'augmentation asymptotique de la durée d'exécution du programme lorsque la quantité de vos données d'entrée augmente vers l'infini. Par exemple, vous comparez le tri d’un tableau de 1 000 éléments et de 10 éléments, et vous devez comprendre comment la durée d’exécution du programme va augmenter. Ou vous devez calculer la longueur d'une chaîne de caractères en allant caractère par caractère et en ajoutant 1 pour chaque caractère : c - 1 a - 2 t - 3 Sa vitesse asymptotique = O(n), où n est le nombre de lettres du mot. Si l'on compte selon ce principe, le temps nécessaire pour compter toute la ligne est proportionnel au nombre de caractères. Compter le nombre de caractères dans une chaîne de 20 caractères prend deux fois plus de temps que compter le nombre de caractères dans une chaîne de dix caractères. Imaginez que dans la variable de longueur vous ayez stocké une valeur égale au nombre de caractères de la chaîne. Par exemple, longueur = 1 000. Pour obtenir la longueur d’une chaîne, vous n’avez besoin que d’accéder à cette variable ; vous n’avez même pas besoin de regarder la chaîne elle-même. Et peu importe comment nous modifions la longueur, nous pouvons toujours accéder à cette variable. Dans ce cas, vitesse asymptotique = O(1). La modification des données d'entrée ne modifie pas la vitesse d'une telle tâche, la recherche s'effectue en un temps constant. Dans ce cas, le programme est asymptotiquement constant. Inconvénient : vous gaspillez de la mémoire informatique en stockant une variable supplémentaire et du temps supplémentaire pour mettre à jour sa valeur. Si vous pensez que le temps linéaire est mauvais, nous pouvons vous assurer que cela peut être bien pire. Par exemple, O(n 2 ). Cette notation signifie qu'à mesure que n grandit, le temps nécessaire pour parcourir les éléments (ou une autre action) augmentera de plus en plus fortement. Mais pour n petit, les algorithmes à vitesse asymptotique O(n 2 ) peuvent fonctionner plus rapidement que les algorithmes à vitesse asymptotique O(n). Mais à un moment donné, la fonction quadratique dépassera la fonction linéaire, il n'y a aucun moyen de contourner ce problème. Une autre complexité asymptotique est le temps logarithmique ou O (log n). À mesure que n augmente, cette fonction augmente très lentement. O(log n) est le temps d'exécution de l'algorithme de recherche binaire classique dans un tableau trié (vous vous souvenez de l'annuaire téléphonique déchiré dans le cours ?). Le tableau est divisé en deux, puis la moitié dans laquelle se trouve l'élément est sélectionnée, et ainsi, en réduisant à chaque fois la zone de recherche de moitié, on recherche l'élément. Que se passe-t-il si nous tombons immédiatement sur ce que nous recherchons, en divisant pour la première fois notre ensemble de données en deux ? Il existe un terme pour le meilleur moment : Omega-large ou Ω(n). Dans le cas d'une recherche binaire = Ω(1) (trouve en temps constant, quelle que soit la taille du tableau). La recherche linéaire s'exécute en temps O(n) et Ω(1) si l'élément recherché est le tout premier. Un autre symbole est thêta (Θ(n)). Il est utilisé lorsque les meilleures et les pires options sont identiques. Cela convient à un exemple où nous avons stocké la longueur d'une chaîne dans une variable distincte, donc pour n'importe quelle longueur, il suffit de faire référence à cette variable. Pour cet algorithme, les meilleurs et les pires cas sont respectivement Ω(1) et O(1). Cela signifie que l’algorithme s’exécute dans le temps Θ(1).
Recherche linéaire
Lorsque vous ouvrez un navigateur web, recherchez une page, une information, des amis sur les réseaux sociaux, vous effectuez une recherche, tout comme lorsque vous cherchez la bonne paire de chaussures dans un magasin. Vous avez probablement remarqué que l'ordre a un impact important sur la façon dont vous effectuez une recherche. Si vous avez toutes vos chemises dans votre placard, il est généralement plus facile de trouver celle dont vous avez besoin parmi elles que parmi celles éparpillées sans système dans toute la pièce. La recherche linéaire est une méthode de recherche séquentielle, un par un. Lorsque vous examinez les résultats de recherche Google de haut en bas, vous utilisez une recherche linéaire. Exemple . Disons que nous avons une liste de nombres : 2 4 0 5 3 7 8 1 et nous devons trouver 0. Nous le voyons tout de suite, mais un programme informatique ne fonctionne pas de cette façon. Elle commence au début de la liste et voit le chiffre 2. Puis elle vérifie : 2=0 ? Ce n'est pas le cas, alors elle continue et passe au deuxième personnage. Là aussi, l'échec l'attend, et ce n'est qu'en troisième position que l'algorithme trouve le nombre requis. Pseudo-code pour la recherche linéaire : La fonction LinearSearch reçoit deux arguments en entrée - la clé key et le tableau array[]. La clé est la valeur souhaitée, dans l'exemple précédent key = 0. Le tableau est une liste de nombres que nous je vais regarder à travers. Si nous ne trouvons rien, la fonction retournera -1 (une position qui n'existe pas dans le tableau). Si la recherche linéaire trouve l'élément souhaité, la fonction renverra la position à laquelle se trouve l'élément souhaité dans le tableau. L’avantage de la recherche linéaire est qu’elle fonctionnera pour n’importe quel tableau, quel que soit l’ordre des éléments : nous parcourrons toujours l’ensemble du tableau. C'est aussi sa faiblesse. Si vous avez besoin de trouver le nombre 198 dans un tableau de 200 nombres triés dans l’ordre, la boucle for passera par 198 étapes. Vous avez probablement déjà deviné quelle méthode fonctionne le mieux pour un tableau trié ?
Recherche binaire et arbres
Imaginez que vous ayez une liste de personnages Disney triés par ordre alphabétique et que vous deviez trouver Mickey Mouse. Linéairement, cela prendrait beaucoup de temps. Et si nous utilisons la « méthode consistant à déchirer le répertoire en deux », nous arrivons directement à Jasmine et nous pouvons supprimer en toute sécurité la première moitié de la liste, réalisant que Mickey ne peut pas être là. En utilisant le même principe, nous supprimons la deuxième colonne. En poursuivant cette stratégie, nous retrouverons Mickey en quelques étapes seulement. Trouvons le nombre 144. Nous divisons la liste en deux et nous arrivons au nombre 13. Nous évaluons si le nombre que nous recherchons est supérieur ou inférieur à 13. 13 < 144, nous pouvons donc ignorer tout ce qui se trouve à gauche de 13 et ce numéro lui-même. Maintenant, notre liste de recherche ressemble à ceci : 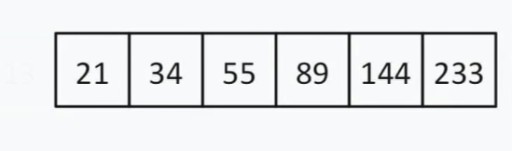il y a un nombre pair d'éléments, nous choisissons donc le principe selon lequel nous sélectionnons le « milieu » (plus proche du début ou de la fin). Disons que nous avons choisi la stratégie de proximité dès le départ. Dans ce cas, notre « milieu » = 55, 55 < 144. Nous supprimons à nouveau la moitié gauche de la liste. Heureusement pour nous, le nombre moyen suivant est 144. Nous en avons trouvé 144 dans un tableau de 13 éléments en utilisant la recherche binaire en seulement trois étapes. Une recherche linéaire traiterait la même situation en 12 étapes maximum. Étant donné que cet algorithme réduit de moitié le nombre d'éléments du tableau à chaque étape, il trouvera celui requis dans un temps asymptotique O(log n), où n est le nombre d'éléments dans la liste. C'est-à-dire, dans notre cas, le temps asymptotique = O(log 13) (c'est un peu plus de trois). Pseudocode de la fonction de recherche binaire : 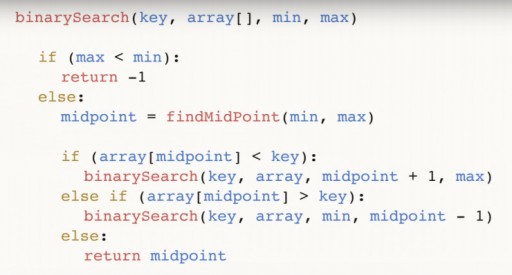La fonction prend 4 arguments en entrée : la clé souhaitée, le tableau de données tableau [], dans lequel se trouve celui souhaité, min et max sont des pointeurs vers le nombre maximum et minimum dans le tableau, qui nous examinons cette étape de l’algorithme. Pour notre exemple, l’image suivante a été initialement donnée : Analysons le code plus en détail. le point médian est notre milieu du tableau. Il dépend des points extrêmes et est centré entre eux. Après avoir trouvé le milieu, nous vérifions s'il est inférieur à notre numéro clé. Si tel est le cas, alors key est également supérieur à n'importe lequel des nombres à gauche du milieu, et nous pouvons appeler à nouveau la fonction binaire, seulement maintenant notre min = point médian + 1. S'il s'avère que clé < point médian, nous pouvons rejeter ce numéro lui-même et tous les chiffres qui se trouvent à sa droite. Et nous appelons une recherche binaire dans le tableau à partir du nombre min et jusqu'à la valeur (point médian – 1). Enfin, troisième branche : si la valeur au milieu n'est ni supérieure ni inférieure à clé, elle n'a d'autre choix que d'être le nombre souhaité. Dans ce cas, nous le rendons et terminons le programme. Enfin, il peut arriver que le numéro que vous recherchez ne soit pas du tout dans le tableau. Pour prendre en compte ce cas, nous effectuons la vérification suivante : Et on retourne (-1) pour indiquer qu'on n'a rien trouvé. Vous savez déjà que la recherche binaire nécessite que le tableau soit trié. Ainsi, si nous avons un tableau non trié dans lequel nous devons trouver un certain élément, nous avons deux options :
Triez la liste et appliquez la recherche binaire
Gardez la liste toujours triée tout en y ajoutant et en supprimant simultanément des éléments.
Une façon de trier les listes consiste à utiliser un arbre de recherche binaire. Un arbre de recherche binaire est une structure de données qui répond aux exigences suivantes :
C'est un arbre (une structure de données qui émule une structure arborescente - elle a une racine et d'autres nœuds (feuilles) reliés par des « branches » ou des arêtes sans cycles)
Chaque nœud a 0, 1 ou 2 enfants
Les sous-arbres gauche et droit sont des arbres de recherche binaires.
Tous les nœuds du sous-arbre gauche d'un nœud arbitraire X ont des valeurs de clé de données inférieures à la valeur de la clé de données du nœud X lui-même.
Tous les nœuds du sous-arbre droit d'un nœud arbitraire X ont des valeurs de clé de données supérieures ou égales à la valeur de la clé de données du nœud X lui-même.
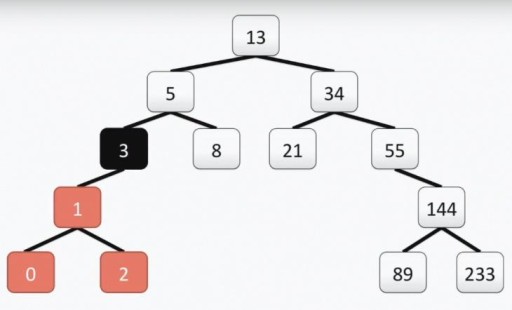Attention : la racine de l'arborescence « programmeur », contrairement à la vraie, se trouve en haut. Chaque cellule est appelée sommet et les sommets sont reliés par des arêtes. La racine de l'arbre est la cellule numéro 13. Le sous-arbre gauche du sommet 3 est mis en évidence en couleur dans l'image ci-dessous : Notre arbre répond à toutes les exigences des arbres binaires. Cela signifie que chacun de ses sous-arbres de gauche ne contient que des valeurs inférieures ou égales à la valeur du sommet, tandis que le sous-arbre de droite ne contient que des valeurs supérieures ou égales à la valeur du sommet. Les sous-arbres gauche et droit sont eux-mêmes des sous-arbres binaires. La méthode de construction d'un arbre binaire n'est pas la seule : ci-dessous dans l'image, vous voyez une autre option pour le même ensemble de nombres, et il peut y en avoir beaucoup dans la pratique. Cette structure permet de réaliser la recherche : on trouve la valeur minimale en se déplaçant à chaque fois du haut vers la gauche et vers le bas. 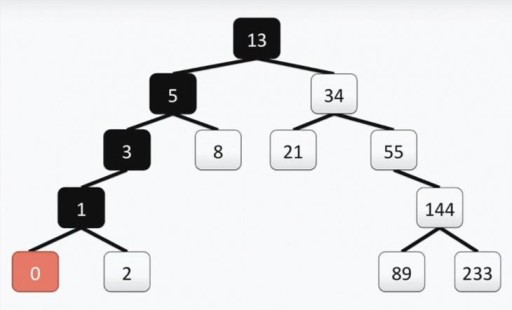Si vous avez besoin de trouver le nombre maximum, on part de haut en bas et vers la droite. Trouver un nombre qui n'est ni le minimum ni le maximum est également assez simple. On descend de la racine vers la gauche ou vers la droite, selon que notre sommet est plus grand ou plus petit que celui que l'on recherche. Ainsi, si nous avons besoin de trouver le nombre 89, nous suivons ce chemin : Vous pouvez également afficher les nombres par ordre de tri. Par exemple, si nous devons afficher tous les nombres par ordre croissant, nous prenons le sous-arbre de gauche et, en partant du sommet le plus à gauche, montons. Ajouter quelque chose à l’arbre est également facile. La principale chose à retenir est la structure. Disons que nous devons ajouter à l'arbre la valeur 7. Allons à la racine et vérifions. Le chiffre 7 < 13, donc on va à gauche. On y voit 5, et on va vers la droite, puisque 7 > 5. De plus, comme 7 > 8 et 8 n'a pas de descendants, on construit une branche de 8 vers la gauche et on y attache 7. Vous pouvez également supprimer des sommets de l'arbre, mais c'est un peu plus compliqué. Il existe trois scénarios de suppression différents que nous devons considérer.
L'option la plus simple : nous devons supprimer un sommet qui n'a pas d'enfant. Par exemple, le chiffre 7 que nous venons d'ajouter. Dans ce cas, nous suivons simplement le chemin vers le sommet avec ce numéro et le supprimons.
Un sommet a un sommet enfant. Dans ce cas, vous pouvez supprimer le sommet souhaité, mais son descendant doit être connecté au « grand-père », c'est-à-dire le sommet à partir duquel son ancêtre immédiat est né. Par exemple, du même arbre, nous devons supprimer le nombre 3. Dans ce cas, nous joignons son descendant, un, avec tout le sous-arbre à 5. Cela se fait simplement, puisque tous les sommets à gauche de 5 seront inférieur à ce nombre (et inférieur au triple distant).
Le cas le plus difficile est celui où le sommet supprimé a deux enfants. Maintenant, la première chose que nous devons faire est de trouver le sommet dans lequel la valeur immédiatement plus grande est cachée, nous devons les échanger, puis supprimer le sommet souhaité. Notez que le prochain sommet de valeur la plus élevée ne peut pas avoir deux enfants, alors son enfant de gauche sera le meilleur candidat pour la valeur suivante. Supprimons de notre arbre le nœud racine 13. Tout d'abord, nous recherchons le nombre le plus proche de 13, qui est supérieur à lui. Il s'agit du 21. Échangez 21 et 13 et supprimez le 13.
Il existe différentes manières de construire des arbres binaires, certaines bonnes, d'autres moins bonnes. Que se passe-t-il si nous essayons de construire un arbre binaire à partir d’une liste triée ? Tous les numéros seront simplement ajoutés à la branche droite du précédent. Si nous voulons trouver un numéro, nous n’aurons d’autre choix que de simplement suivre la chaîne. Ce n'est pas mieux qu'une recherche linéaire. Il existe d'autres structures de données plus complexes. Mais nous ne les considérerons pas pour l’instant. Disons simplement que pour résoudre le problème de la construction d'un arbre à partir d'une liste triée, vous pouvez mélanger aléatoirement les données d'entrée.
Algorithmes de tri
Il existe toute une série de chiffres. Nous devons faire le tri. Pour plus de simplicité, nous supposerons que nous trions les entiers par ordre croissant (du plus petit au plus grand). Il existe plusieurs manières connues d'accomplir ce processus. De plus, vous pouvez toujours imaginer le sujet et proposer une modification de l'algorithme.
Tri par sélection
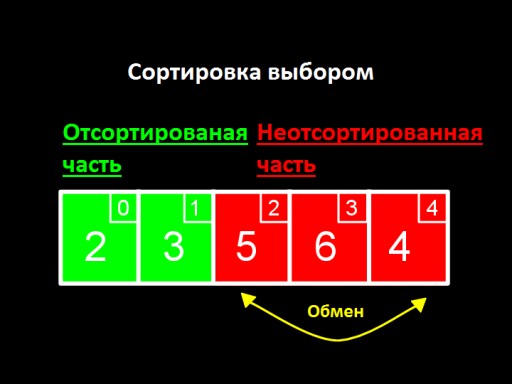L'idée principale est de diviser notre liste en deux parties, triées et non triées. A chaque étape de l'algorithme, un nouveau numéro est déplacé de la partie non triée vers la partie triée, et ainsi de suite jusqu'à ce que tous les numéros soient dans la partie triée.
Trouvez la valeur minimale non triée.
Nous échangeons cette valeur avec la première valeur non triée, la plaçant ainsi à la fin du tableau trié.
S'il reste des valeurs non triées, revenez à l'étape 1.
Dans un premier temps, toutes les valeurs ne sont pas triées. Appelons la partie non triée Non triée et la partie triée Triée (ce ne sont que des mots anglais, et nous le faisons uniquement parce que Sorté est beaucoup plus court que « Partie triée » et sera plus beau en images). Nous trouvons le nombre minimum dans la partie non triée du tableau (c'est-à-dire à cette étape - dans l'ensemble du tableau). Ce nombre est 2. Maintenant, nous le remplaçons par le premier parmi ceux non triés et le plaçons à la fin du tableau trié (à cette étape - en premier lieu). Dans cette étape, il s'agit du premier nombre du tableau, c'est-à-dire 3. Deuxième étape. Nous ne regardons pas le chiffre 2 ; il est déjà dans le sous-tableau trié. On commence à chercher le minimum, à partir du deuxième élément, c'est 5. On s'assure que 3 est le minimum parmi les non triés, 5 est le premier parmi les non triés. Nous les échangeons et en ajoutons 3 au sous-tableau trié. Dans la troisième étape , nous voyons que le plus petit nombre dans le sous-tableau non trié est 4. Nous le modifions avec le premier nombre parmi les nombres non triés - 5. Dans la quatrième étape, nous constatons que dans le tableau non trié, le plus petit nombre est 5. Nous le changeons de 6 et l'ajoutons au sous-tableau trié. 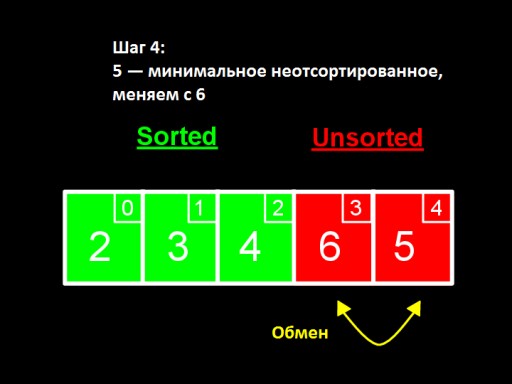Lorsqu'il ne reste qu'un seul nombre parmi les non triés (le plus grand), cela signifie que tout le tableau est trié ! 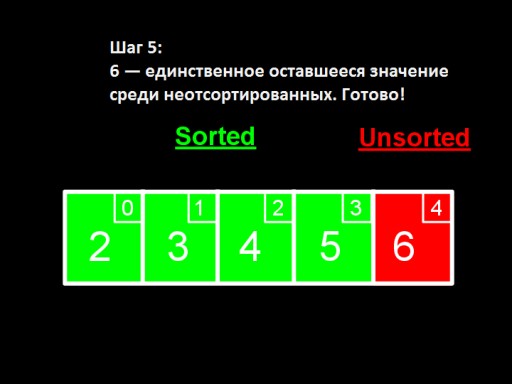Voici à quoi ressemble l'implémentation du tableau dans le code. Essayez de le faire vous-même. Dans le meilleur comme dans le pire des cas, pour trouver l'élément non trié minimum, nous devons comparer chaque élément avec chaque élément du tableau non trié, et nous le ferons à chaque itération. Mais nous n’avons pas besoin de visualiser la liste entière, mais seulement la partie non triée. Est-ce que cela change la vitesse de l’algorithme ? Dans la première étape, pour un tableau de 5 éléments, nous effectuons 4 comparaisons, dans la deuxième - 3, dans la troisième - 2. Pour obtenir le nombre de comparaisons, nous devons additionner tous ces nombres. Nous obtenons la somme. Ainsi, la vitesse attendue de l'algorithme dans le meilleur et le pire des cas est Θ(n 2 ). Ce n’est pas l’algorithme le plus efficace ! Cependant, à des fins éducatives et pour de petits ensembles de données, cela est tout à fait applicable.
Tri à bulles
L'algorithme de tri à bulles est l'un des plus simples. Nous parcourons tout le tableau et comparons 2 éléments voisins. S'ils sont dans le mauvais ordre, nous les échangeons. Au premier passage, le plus petit élément apparaîtra (« float ») à la fin (si on trie par ordre décroissant). Répétez la première étape si au moins un échange a été effectué à l'étape précédente. Trions le tableau. Étape 1 : parcourir le tableau. L'algorithme commence par les deux premiers éléments, 8 et 6, et vérifie s'ils sont dans le bon ordre. 8 > 6, donc on les échange. Ensuite, nous regardons les deuxième et troisième éléments, maintenant ce sont 8 et 4. Pour les mêmes raisons, nous les échangeons. Pour la troisième fois on compare 8 et 2. Au total, on fait trois échanges (8, 6), (8, 4), (8, 2). La valeur 8 "flottait" jusqu'à la fin de la liste dans la bonne position. Étape 2 : échangez (6,4) et (6,2). Le 6 se trouve désormais en avant-dernière position, et il n'est pas nécessaire de le comparer avec la « queue » déjà triée de la liste. Étape 3 : échangez 4 et 2. Les quatre « flottent » à la place qui leur revient. Étape 4 : on parcourt le tableau, mais nous n'avons rien à changer. Cela indique que le tableau est complètement trié. 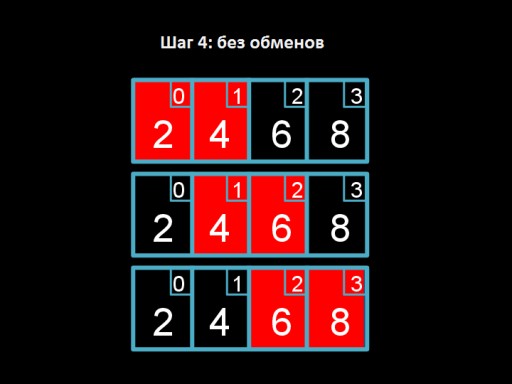Et voici le code de l'algorithme. Essayez de l'implémenter en C ! Le tri à bulles prend un temps O(n 2 ) dans le pire des cas (tous les nombres sont faux), puisque nous devons effectuer n étapes à chaque itération, qui sont également au nombre de n. En fait, comme dans le cas de l'algorithme de tri par sélection, le temps sera légèrement inférieur (n 2 /2 – n/2), mais cela peut être négligé. Dans le meilleur des cas (si tous les éléments sont déjà en place), on peut le faire en n étapes, soit Ω(n), puisque nous aurons juste besoin de parcourir le tableau une fois et de nous assurer que tous les éléments sont en place (c'est-à-dire même n-1 éléments).
Tri par insertion
L'idée principale de cet algorithme est de diviser notre tableau en deux parties, triées et non triées. A chaque étape de l'algorithme, le nombre passe de la partie non triée à la partie triée. Voyons comment fonctionne le tri par insertion à l'aide de l'exemple ci-dessous. Avant de commencer, tous les éléments sont considérés comme non triés. Étape 1 : prenez la première valeur non triée (3) et insérez-la dans le sous-tableau trié. À cette étape, l'ensemble du sous-tableau trié, son début et sa fin seront exactement les trois. Étape 2 : Puisque 3 > 5, nous allons insérer 5 dans le sous-tableau trié à droite de 3. Étape 3 : Nous travaillons maintenant sur l'insertion du nombre 2 dans notre tableau trié. On compare 2 avec les valeurs de droite à gauche pour trouver la bonne position. Depuis 2 < 5 et 2 < 3 et nous avons atteint le début du sous-tableau trié. Il faut donc insérer 2 à gauche de 3. Pour cela, déplacez 3 et 5 vers la droite pour qu'il y ait de la place pour le 2 et insérez-le au début du tableau. Étape 4. Nous avons de la chance : 6 > 5, nous pouvons donc insérer ce nombre juste après le chiffre 5. Étape 5. 4 < 6 et 4 < 5, mais 4 > 3. Nous savons donc que 4 doit être inséré pour à droite de 3. Encore une fois, on est obligé de déplacer 5 et 6 vers la droite pour créer un écart pour 4. C'est fait ! Algorithme généralisé : prenez chaque élément non trié de n et comparez-le avec les valeurs du sous-tableau trié de droite à gauche jusqu'à ce que nous trouvions une position appropriée pour n (c'est-à-dire le moment où nous trouvons le premier nombre inférieur à n) . Ensuite, nous décalons tous les éléments triés qui se trouvent à droite de ce nombre vers la droite pour faire de la place à notre n, et nous l'insérons là, élargissant ainsi la partie triée du tableau. Pour chaque élément n non trié il vous faut :
Déterminer l'emplacement dans la partie triée du tableau où n doit être inséré
Déplacez les éléments triés vers la droite pour créer un espace pour n
Insérez n dans l'espace résultant dans la partie triée du tableau.
Et voici le code ! Nous vous recommandons d'écrire votre propre version du programme de tri.
Vitesse asymptotique de l'algorithme
Dans le pire des cas, nous ferons une comparaison avec le deuxième élément, deux comparaisons avec le troisième, et ainsi de suite. Ainsi notre vitesse est O(n 2 ). Au mieux, nous travaillerons avec un tableau déjà trié. La partie triée, que l’on construit de gauche à droite sans insertions ni mouvements d’éléments, prendra un temps Ω(n).
Tri par fusion
Cet algorithme est récursif ; il divise un grand problème de tri en sous-tâches, dont l'exécution le rapproche de la résolution du grand problème d'origine. L'idée principale est de diviser un tableau non trié en deux parties et de trier les moitiés individuelles de manière récursive. Disons que nous avons n éléments à trier. Si n < 2, nous terminons le tri, sinon nous trions séparément les parties gauche et droite du tableau, puis les combinons. Trions le tableau. Divisons-le en deux parties et continuons à diviser jusqu'à obtenir des sous-tableaux de taille 1, qui sont évidemment triés. Deux sous-tableaux triés peuvent être fusionnés en un temps O(n) à l'aide d'un algorithme simple : supprimez le plus petit nombre au début de chaque sous-tableau et insérez-le dans le tableau fusionné. Répétez jusqu'à ce que tous les éléments aient disparu. Le tri par fusion prend un temps O(nlog n) pour tous les cas. Pendant que nous divisons les tableaux en moitiés à chaque niveau de récursion, nous obtenons log n. Ensuite, la fusion des sous-tableaux ne nécessite que n comparaisons. Donc O(nlog n). Les meilleurs et les pires cas pour le tri par fusion sont les mêmes, le temps d'exécution attendu de l'algorithme = Θ (nlog n). Cet algorithme est le plus efficace parmi ceux considérés.
Mais à un moment donné, la fonction quadratique dépassera la fonction linéaire, il n'y a aucun moyen de contourner ce problème. Une autre complexité asymptotique est le temps logarithmique ou O (log n). À mesure que n augmente, cette fonction augmente très lentement. O(log n) est le temps d'exécution de l'algorithme de recherche binaire classique dans un tableau trié (vous vous souvenez de l'annuaire téléphonique déchiré dans le cours ?). Le tableau est divisé en deux, puis la moitié dans laquelle se trouve l'élément est sélectionnée, et ainsi, en réduisant à chaque fois la zone de recherche de moitié, on recherche l'élément. 
Que se passe-t-il si nous tombons immédiatement sur ce que nous recherchons, en divisant pour la première fois notre ensemble de données en deux ? Il existe un terme pour le meilleur moment : Omega-large ou Ω(n). Dans le cas d'une recherche binaire = Ω(1) (trouve en temps constant, quelle que soit la taille du tableau). La recherche linéaire s'exécute en temps O(n) et Ω(1) si l'élément recherché est le tout premier. Un autre symbole est thêta (Θ(n)). Il est utilisé lorsque les meilleures et les pires options sont identiques. Cela convient à un exemple où nous avons stocké la longueur d'une chaîne dans une variable distincte, donc pour n'importe quelle longueur, il suffit de faire référence à cette variable. Pour cet algorithme, les meilleurs et les pires cas sont respectivement Ω(1) et O(1). Cela signifie que l’algorithme s’exécute dans le temps Θ(1).
fonction LinearSearch reçoit deux arguments en entrée - la clé key et le tableau array[]. La clé est la valeur souhaitée, dans l'exemple précédent key = 0. Le tableau est une liste de nombres que nous je vais regarder à travers. Si nous ne trouvons rien, la fonction retournera -1 (une position qui n'existe pas dans le tableau). Si la recherche linéaire trouve l'élément souhaité, la fonction renverra la position à laquelle se trouve l'élément souhaité dans le tableau. L’avantage de la recherche linéaire est qu’elle fonctionnera pour n’importe quel tableau, quel que soit l’ordre des éléments : nous parcourrons toujours l’ensemble du tableau. C'est aussi sa faiblesse. Si vous avez besoin de trouver le nombre 198 dans un tableau de 200 nombres triés dans l’ordre, la boucle for passera par 198 étapes. 
Vous avez probablement déjà deviné quelle méthode fonctionne le mieux pour un tableau trié ?
Linéairement, cela prendrait beaucoup de temps. Et si nous utilisons la « méthode consistant à déchirer le répertoire en deux », nous arrivons directement à Jasmine et nous pouvons supprimer en toute sécurité la première moitié de la liste, réalisant que Mickey ne peut pas être là. 
En utilisant le même principe, nous supprimons la deuxième colonne. En poursuivant cette stratégie, nous retrouverons Mickey en quelques étapes seulement. 
Trouvons le nombre 144. Nous divisons la liste en deux et nous arrivons au nombre 13. Nous évaluons si le nombre que nous recherchons est supérieur ou inférieur à 13. 13 < 144, nous pouvons donc ignorer tout ce qui se trouve à gauche 
de 13 et ce numéro lui-même. Maintenant, notre liste de recherche ressemble à ceci : 
il y a un nombre pair d'éléments, nous choisissons donc le principe selon lequel nous sélectionnons le « milieu » (plus proche du début ou de la fin). Disons que nous avons choisi la stratégie de proximité dès le départ. Dans ce cas, notre « milieu » = 55, 
55 < 144. Nous supprimons à nouveau la moitié gauche de la liste. Heureusement pour nous, le nombre moyen suivant est 144. 
Nous en avons trouvé 144 dans un tableau de 13 éléments en utilisant la recherche binaire en seulement trois étapes. Une recherche linéaire traiterait la même situation en 12 étapes maximum. Étant donné que cet algorithme réduit de moitié le nombre d'éléments du tableau à chaque étape, il trouvera celui requis dans un temps asymptotique O(log n), où n est le nombre d'éléments dans la liste. C'est-à-dire, dans notre cas, le temps asymptotique = O(log 13) (c'est un peu plus de trois). Pseudocode de la fonction de recherche binaire : 
La fonction prend 4 arguments en entrée : la clé souhaitée, le tableau de données tableau [], dans lequel se trouve celui souhaité, min et max sont des pointeurs vers le nombre maximum et minimum dans le tableau, qui nous examinons cette étape de l’algorithme. Pour notre exemple, l’image suivante a été initialement donnée : 
Analysons le code plus en détail. le point médian est notre milieu du tableau. Il dépend des points extrêmes et est centré entre eux. Après avoir trouvé le milieu, nous vérifions s'il est inférieur à notre numéro clé. 
Si tel est le cas, alors key est également supérieur à n'importe lequel des nombres à gauche du milieu, et nous pouvons appeler à nouveau la fonction binaire, seulement maintenant notre min = point médian + 1. S'il s'avère que clé < point médian, nous pouvons rejeter ce numéro lui-même et tous les chiffres qui se trouvent à sa droite. Et nous appelons une recherche binaire dans le tableau à partir du nombre min et jusqu'à la valeur (point médian – 1). 
Enfin, troisième branche : si la valeur au milieu n'est ni supérieure ni inférieure à clé, elle n'a d'autre choix que d'être le nombre souhaité. Dans ce cas, nous le rendons et terminons le programme. 
Enfin, il peut arriver que le numéro que vous recherchez ne soit pas du tout dans le tableau. Pour prendre en compte ce cas, nous effectuons la vérification suivante : 
Et on retourne (-1) pour indiquer qu'on n'a rien trouvé. Vous savez déjà que la recherche binaire nécessite que le tableau soit trié. Ainsi, si nous avons un tableau non trié dans lequel nous devons trouver un certain élément, nous avons deux options :
Attention : la racine de l'arborescence « programmeur », contrairement à la vraie, se trouve en haut. Chaque cellule est appelée sommet et les sommets sont reliés par des arêtes. La racine de l'arbre est la cellule numéro 13. Le sous-arbre gauche du sommet 3 est mis en évidence en couleur dans l'image ci-dessous : 
Notre arbre répond à toutes les exigences des arbres binaires. Cela signifie que chacun de ses sous-arbres de gauche ne contient que des valeurs inférieures ou égales à la valeur du sommet, tandis que le sous-arbre de droite ne contient que des valeurs supérieures ou égales à la valeur du sommet. Les sous-arbres gauche et droit sont eux-mêmes des sous-arbres binaires. La méthode de construction d'un arbre binaire n'est pas la seule : ci-dessous dans l'image, vous voyez une autre option pour le même ensemble de nombres, et il peut y en avoir beaucoup dans la pratique. 
Cette structure permet de réaliser la recherche : on trouve la valeur minimale en se déplaçant à chaque fois du haut vers la gauche et vers le bas. 
Si vous avez besoin de trouver le nombre maximum, on part de haut en bas et vers la droite. Trouver un nombre qui n'est ni le minimum ni le maximum est également assez simple. On descend de la racine vers la gauche ou vers la droite, selon que notre sommet est plus grand ou plus petit que celui que l'on recherche. Ainsi, si nous avons besoin de trouver le nombre 89, nous suivons ce chemin : 
Vous pouvez également afficher les nombres par ordre de tri. Par exemple, si nous devons afficher tous les nombres par ordre croissant, nous prenons le sous-arbre de gauche et, en partant du sommet le plus à gauche, montons. Ajouter quelque chose à l’arbre est également facile. La principale chose à retenir est la structure. Disons que nous devons ajouter à l'arbre la valeur 7. Allons à la racine et vérifions. Le chiffre 7 < 13, donc on va à gauche. On y voit 5, et on va vers la droite, puisque 7 > 5. De plus, comme 7 > 8 et 8 n'a pas de descendants, on construit une branche de 8 vers la gauche et on y attache 7. Vous pouvez également supprimer des sommets 
de l'arbre, mais c'est un peu plus compliqué. Il existe trois scénarios de suppression différents que nous devons considérer.
Tous les numéros seront simplement ajoutés à la branche droite du précédent. Si nous voulons trouver un numéro, nous n’aurons d’autre choix que de simplement suivre la chaîne. 
Ce n'est pas mieux qu'une recherche linéaire. Il existe d'autres structures de données plus complexes. Mais nous ne les considérerons pas pour l’instant. Disons simplement que pour résoudre le problème de la construction d'un arbre à partir d'une liste triée, vous pouvez mélanger aléatoirement les données d'entrée.
L'idée principale est de diviser notre liste en deux parties, triées et non triées. A chaque étape de l'algorithme, un nouveau numéro est déplacé de la partie non triée vers la partie triée, et ainsi de suite jusqu'à ce que tous les numéros soient dans la partie triée.
Nous trouvons le nombre minimum dans la partie non triée du tableau (c'est-à-dire à cette étape - dans l'ensemble du tableau). Ce nombre est 2. Maintenant, nous le remplaçons par le premier parmi ceux non triés et le plaçons à la fin du tableau trié (à cette étape - en premier lieu). Dans cette étape, il s'agit du premier nombre du tableau, c'est-à-dire 3. 
Deuxième étape. Nous ne regardons pas le chiffre 2 ; il est déjà dans le sous-tableau trié. On commence à chercher le minimum, à partir du deuxième élément, c'est 5. On s'assure que 3 est le minimum parmi les non triés, 5 est le premier parmi les non triés. Nous les échangeons et en ajoutons 3 au sous-tableau trié. 
Dans la troisième étape , nous voyons que le plus petit nombre dans le sous-tableau non trié est 4. Nous le modifions avec le premier nombre parmi les nombres non triés - 5. 
Dans la quatrième étape, nous constatons que dans le tableau non trié, le plus petit nombre est 5. Nous le changeons de 6 et l'ajoutons au sous-tableau trié. 
Lorsqu'il ne reste qu'un seul nombre parmi les non triés (le plus grand), cela signifie que tout le tableau est trié ! 
Voici à quoi ressemble l'implémentation du tableau dans le code. Essayez de le faire vous-même. 
Dans le meilleur comme dans le pire des cas, pour trouver l'élément non trié minimum, nous devons comparer chaque élément avec chaque élément du tableau non trié, et nous le ferons à chaque itération. Mais nous n’avons pas besoin de visualiser la liste entière, mais seulement la partie non triée. Est-ce que cela change la vitesse de l’algorithme ? Dans la première étape, pour un tableau de 5 éléments, nous effectuons 4 comparaisons, dans la deuxième - 3, dans la troisième - 2. Pour obtenir le nombre de comparaisons, nous devons additionner tous ces nombres. Nous obtenons la somme. 
Ainsi, la vitesse attendue de l'algorithme dans le meilleur et le pire des cas est Θ(n 2 ). Ce n’est pas l’algorithme le plus efficace ! Cependant, à des fins éducatives et pour de petits ensembles de données, cela est tout à fait applicable.
Étape 1 : parcourir le tableau. L'algorithme commence par les deux premiers éléments, 8 et 6, et vérifie s'ils sont dans le bon ordre. 8 > 6, donc on les échange. Ensuite, nous regardons les deuxième et troisième éléments, maintenant ce sont 8 et 4. Pour les mêmes raisons, nous les échangeons. Pour la troisième fois on compare 8 et 2. Au total, on fait trois échanges (8, 6), (8, 4), (8, 2). La valeur 8 "flottait" jusqu'à la fin de la liste dans la bonne position. 
Étape 2 : échangez (6,4) et (6,2). Le 6 se trouve désormais en avant-dernière position, et il n'est pas nécessaire de le comparer avec la « queue » déjà triée de la liste. 
Étape 3 : échangez 4 et 2. Les quatre « flottent » à la place qui leur revient. 
Étape 4 : on parcourt le tableau, mais nous n'avons rien à changer. Cela indique que le tableau est complètement trié. 
Et voici le code de l'algorithme. Essayez de l'implémenter en C ! 
Le tri à bulles prend un temps O(n 2 ) dans le pire des cas (tous les nombres sont faux), puisque nous devons effectuer n étapes à chaque itération, qui sont également au nombre de n. En fait, comme dans le cas de l'algorithme de tri par sélection, le temps sera légèrement inférieur (n 2 /2 – n/2), mais cela peut être négligé. Dans le meilleur des cas (si tous les éléments sont déjà en place), on peut le faire en n étapes, soit Ω(n), puisque nous aurons juste besoin de parcourir le tableau une fois et de nous assurer que tous les éléments sont en place (c'est-à-dire même n-1 éléments).
Voyons comment fonctionne le tri par insertion à l'aide de l'exemple ci-dessous. Avant de commencer, tous les éléments sont considérés comme non triés. 
Étape 1 : prenez la première valeur non triée (3) et insérez-la dans le sous-tableau trié. À cette étape, l'ensemble du sous-tableau trié, son début et sa fin seront exactement les trois. 
Étape 2 : Puisque 3 > 5, nous allons insérer 5 dans le sous-tableau trié à droite de 3. 
Étape 3 : Nous travaillons maintenant sur l'insertion du nombre 2 dans notre tableau trié. On compare 2 avec les valeurs de droite à gauche pour trouver la bonne position. Depuis 2 < 5 et 2 < 3 et nous avons atteint le début du sous-tableau trié. Il faut donc insérer 2 à gauche de 3. Pour cela, déplacez 3 et 5 vers la droite pour qu'il y ait de la place pour le 2 et insérez-le au début du tableau. 
Étape 4. Nous avons de la chance : 6 > 5, nous pouvons donc insérer ce nombre juste après le chiffre 5. 
Étape 5. 4 < 6 et 4 < 5, mais 4 > 3. Nous savons donc que 4 doit être inséré pour à droite de 3. Encore une fois, on est obligé de déplacer 5 et 6 vers la droite pour créer un écart pour 4. 
C'est fait ! Algorithme généralisé : prenez chaque élément non trié de n et comparez-le avec les valeurs du sous-tableau trié de droite à gauche jusqu'à ce que nous trouvions une position appropriée pour n (c'est-à-dire le moment où nous trouvons le premier nombre inférieur à n) . Ensuite, nous décalons tous les éléments triés qui se trouvent à droite de ce nombre vers la droite pour faire de la place à notre n, et nous l'insérons là, élargissant ainsi la partie triée du tableau. Pour chaque élément n non trié il vous faut :
Disons que nous avons n éléments à trier. Si n < 2, nous terminons le tri, sinon nous trions séparément les parties gauche et droite du tableau, puis les combinons. Trions le tableau. 
Divisons-le en deux parties et continuons à diviser jusqu'à obtenir des sous-tableaux de taille 1, qui sont évidemment triés. 
Deux sous-tableaux triés peuvent être fusionnés en un temps O(n) à l'aide d'un algorithme simple : supprimez le plus petit nombre au début de chaque sous-tableau et insérez-le dans le tableau fusionné. Répétez jusqu'à ce que tous les éléments aient disparu. 
Le tri par fusion prend un temps O(nlog n) pour tous les cas. Pendant que nous divisons les tableaux en moitiés à chaque niveau de récursion, nous obtenons log n. Ensuite, la fusion des sous-tableaux ne nécessite que n comparaisons. Donc O(nlog n). Les meilleurs et les pires cas pour le tri par fusion sont les mêmes, le temps d'exécution attendu de l'algorithme = Θ (nlog n). Cet algorithme est le plus efficace parmi ceux considérés. 
GO TO FULL VERSION