Bahan Tambahan CS50 (Minggu 3, Kuliah 7 dan 8): Notasi Asimtotik, Algoritma Isih dan Carian

Kuliah dari kursus Harvard mengenai asas pengaturcaraan tugasan CS50 CS50, minggu 3, bahagian 1 Tugasan CS50, minggu 3, bahagian 2

Notasi asimptotik

Mengukur kelajuan algoritma dalam masa nyata—dalam saat dan minit—bukanlah mudah. Satu program mungkin berjalan lebih perlahan daripada yang lain bukan kerana ketidakcekapannya sendiri, tetapi kerana kelembapan sistem pengendalian, ketidakserasian dengan perkakasan, memori komputer diduduki oleh proses lain... Untuk mengukur keberkesanan algoritma, konsep sejagat telah dicipta , tanpa mengira persekitaran di mana program dijalankan. Kerumitan asimptotik masalah diukur menggunakan tatatanda Big O. Biarkan f(x) dan g(x) sebagai fungsi yang ditakrifkan dalam kejiranan tertentu x0, dan g tidak hilang di sana. Maka f ialah “O” lebih besar daripada g untuk (x -> x0) jika terdapat pemalar C> 0 , bahawa untuk semua x dari beberapa kejiranan titik x0, ketaksamaan berlaku. |f(x)| <= C |g(x)| Sedikit kurang ketat: f ialah “O” lebih besar daripada g jika terdapat pemalar C>0, yang untuk semua x > x0 f(x) <= C*g(x) Jangan takut definisi formal! Pada asasnya, ia menentukan peningkatan asimptotik dalam masa berjalan program apabila jumlah data input anda berkembang ke arah infiniti. Sebagai contoh, anda sedang membandingkan menyusun tatasusunan 1000 elemen dan 10 elemen, dan anda perlu memahami cara masa berjalan program akan meningkat. Atau anda perlu mengira panjang rentetan aksara dengan menggunakan aksara demi aksara dan menambah 1 untuk setiap aksara: c - 1 a - 2 t - 3 Kelajuan asimptotiknya = O(n), dengan n ialah bilangan huruf dalam perkataan. Jika anda mengira mengikut prinsip ini, masa yang diperlukan untuk mengira keseluruhan baris adalah berkadar dengan bilangan aksara. Mengira bilangan aksara dalam rentetan 20 aksara mengambil masa dua kali lebih lama daripada mengira bilangan aksara dalam rentetan sepuluh aksara. Bayangkan bahawa dalam pembolehubah panjang anda menyimpan nilai yang sama dengan bilangan aksara dalam rentetan. Contohnya, panjang = 1000. Untuk mendapatkan panjang rentetan, anda hanya memerlukan akses kepada pembolehubah ini; anda tidak perlu melihat rentetan itu sendiri. Dan tidak kira bagaimana kita menukar panjang, kita sentiasa boleh mengakses pembolehubah ini. Dalam kes ini, kelajuan asimptotik = O(1). Menukar data input tidak mengubah kelajuan tugas sedemikian; carian selesai dalam masa yang tetap. Dalam kes ini, program adalah malar tanpa gejala. Kelemahan: Anda membazir memori komputer menyimpan pembolehubah tambahan dan masa tambahan mengemas kini nilainya. Jika anda berpendapat bahawa masa linear adalah buruk, kami boleh memberi jaminan bahawa masa itu boleh menjadi lebih teruk. Contohnya, O(n ² ). Notasi ini bermaksud bahawa apabila n berkembang, masa yang diperlukan untuk lelaran melalui elemen (atau tindakan lain) akan berkembang lebih dan lebih mendadak. Tetapi untuk n kecil, algoritma dengan kelajuan asimptotik O(n ² ) boleh berfungsi lebih cepat daripada algoritma dengan kelajuan asimptotik O(n). Tetapi pada satu ketika fungsi kuadratik akan mengatasi yang linear, tidak ada jalan untuk mengatasinya. Satu lagi kerumitan asimptotik ialah masa logaritma atau O(log n). Apabila n meningkat, fungsi ini meningkat dengan sangat perlahan. O(log n) ialah masa berjalan bagi algoritma carian binari klasik dalam tatasusunan yang disusun (ingat direktori telefon yang koyak dalam kuliah?). Tatasusunan dibahagikan kepada dua, kemudian separuh di mana elemen terletak dipilih, dan oleh itu, setiap kali mengurangkan kawasan carian sebanyak separuh, kami mencari elemen tersebut. Apakah yang akan berlaku jika kita serta-merta terjumpa apa yang kita cari, membahagikan tatasusunan data kita kepada separuh buat kali pertama? Terdapat istilah untuk masa terbaik - Omega-besar atau Ω(n). Dalam kes carian binari = Ω(1) (mencari dalam masa tetap, tanpa mengira saiz tatasusunan). Carian linear berjalan dalam masa O(n) dan Ω(1) jika elemen yang dicari adalah yang pertama. Simbol lain ialah theta (Θ(n)). Ia digunakan apabila pilihan terbaik dan terburuk adalah sama. Ini sesuai untuk contoh di mana kami menyimpan panjang rentetan dalam pembolehubah yang berasingan, jadi untuk sebarang panjang ia cukup untuk merujuk kepada pembolehubah ini. Untuk algoritma ini, kes terbaik dan terburuk ialah Ω(1) dan O(1), masing-masing. Ini bermakna bahawa algoritma berjalan dalam masa Θ(1).

Carian linear

Apabila anda membuka penyemak imbas web, cari halaman, maklumat, rakan di rangkaian sosial, anda sedang melakukan carian, sama seperti ketika cuba mencari pasangan kasut yang sesuai di kedai. Anda mungkin perasan bahawa keteraturan mempunyai kesan yang besar pada cara anda mencari. Jika anda mempunyai semua baju anda di dalam almari anda, biasanya lebih mudah untuk mencari baju yang anda perlukan di antara mereka daripada yang bertaburan tanpa sistem di seluruh bilik. Carian linear ialah kaedah carian berurutan, satu demi satu. Apabila anda menyemak hasil carian Google dari atas ke bawah, anda menggunakan carian linear. Contoh . Katakan kita mempunyai senarai nombor: 2 4 0 5 3 7 8 1 Dan kita perlu mencari 0. Kita melihatnya serta-merta, tetapi program komputer tidak berfungsi seperti itu. Dia bermula pada permulaan senarai dan melihat nombor 2. Kemudian dia menyemak, 2=0? Tidak, jadi dia meneruskan dan beralih kepada watak kedua. Kegagalan menantinya di sana juga, dan hanya di kedudukan ketiga algoritma mencari nombor yang diperlukan. Pseudo-code untuk carian linear: Fungsi linearSearch menerima dua argumen sebagai input - kunci kekunci dan tatasusunan[]. Kunci ialah nilai yang diingini, dalam kekunci contoh sebelumnya = 0. Tatasusunan ialah senarai nombor yang kita akan melihat melalui. Jika kita tidak menemui apa-apa, fungsi akan kembali -1 (kedudukan yang tidak wujud dalam tatasusunan). Jika carian linear menjumpai elemen yang dikehendaki, fungsi akan mengembalikan kedudukan di mana elemen yang dikehendaki terletak dalam tatasusunan. Perkara yang baik tentang carian linear ialah ia akan berfungsi untuk mana-mana tatasusunan, tanpa mengira susunan elemen: kami masih akan melalui keseluruhan tatasusunan. Ini juga kelemahannya. Jika anda perlu mencari nombor 198 dalam susunan 200 nombor yang disusun mengikut tertib, gelung for akan melalui 198 langkah. Anda mungkin sudah meneka kaedah mana yang berfungsi lebih baik untuk tatasusunan yang diisih?

Carian binari dan pokok

Bayangkan anda mempunyai senarai watak Disney yang disusun mengikut abjad dan anda perlu mencari Mickey Mouse. Secara linear ia akan mengambil masa yang lama. Dan jika kita menggunakan "kaedah mengoyakkan direktori kepada separuh", kita terus ke Jasmine, dan kita boleh membuang separuh pertama senarai dengan selamat, menyedari bahawa Mickey tidak boleh berada di sana. Menggunakan prinsip yang sama, kami membuang lajur kedua. Meneruskan strategi ini, kami akan menemui Mickey dalam beberapa langkah sahaja. Mari cari nombor 144. Kami membahagikan senarai itu kepada separuh, dan kami sampai ke nombor 13. Kami menilai sama ada nombor yang kami cari lebih besar atau kurang daripada 13. 13 < 144, jadi kami boleh mengabaikan segala-galanya di sebelah kiri 13 dan nombor ini sendiri. Kini senarai carian kami kelihatan seperti ini: 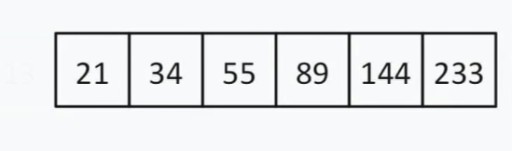Terdapat bilangan elemen genap, jadi kami memilih prinsip yang kami gunakan untuk memilih "tengah" (lebih dekat dengan permulaan atau akhir). Katakan kita memilih strategi berdekatan dengan permulaan. Dalam kes ini, "tengah" kami = 55. 55 < 144. Kami membuang separuh kiri senarai sekali lagi. Nasib baik bagi kami, nombor purata seterusnya ialah 144. Kami mendapati 144 dalam tatasusunan 13 elemen menggunakan carian binari dalam tiga langkah sahaja. Carian linear akan mengendalikan situasi yang sama dalam sebanyak 12 langkah. Memandangkan algoritma ini mengurangkan bilangan elemen dalam tatasusunan sebanyak separuh pada setiap langkah, ia akan mencari satu yang diperlukan dalam masa asimptotik O(log n), di mana n ialah bilangan elemen dalam senarai. Iaitu, dalam kes kami, masa asimptotik = O(log 13) (ini lebih sedikit daripada tiga). Pseudokod bagi fungsi carian binari: 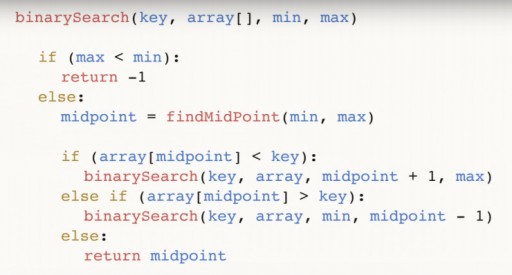Fungsi ini mengambil 4 argumen sebagai input: kunci yang diingini, tatasusunan data [], di mana yang dikehendaki terletak, min dan maks ialah penunjuk kepada nombor maksimum dan minimum dalam tatasusunan, yang kita sedang melihat pada langkah algoritma ini. Untuk contoh kami, gambar berikut pada mulanya diberikan: Mari analisa kod dengan lebih lanjut. titik tengah ialah tengah tatasusunan kami. Ia bergantung pada titik ekstrem dan berpusat di antara mereka. Selepas kami menemui bahagian tengah, kami menyemak sama ada ia kurang daripada nombor kunci kami. Jika ya, maka kunci juga lebih besar daripada mana-mana nombor di sebelah kiri tengah, dan kita boleh memanggil fungsi binari sekali lagi, hanya sekarang min = titik tengah + 1 kami. Jika ternyata kunci itu < titik tengah, kita boleh membuang nombor itu sendiri dan semua nombor , terletak di sebelah kanannya. Dan kami memanggil carian binari melalui tatasusunan dari nombor min dan sehingga nilai (titik tengah - 1). Akhir sekali, cawangan ketiga: jika nilai dalam titik tengah tidak lebih besar atau kurang daripada kunci, ia tidak mempunyai pilihan selain menjadi nombor yang dikehendaki. Dalam kes ini, kami mengembalikannya dan menyelesaikan program. Akhir sekali, mungkin berlaku bahawa nombor yang anda cari tiada dalam tatasusunan sama sekali. Untuk mengambil kira kes ini, kami melakukan pemeriksaan berikut: Dan kami kembali (-1) untuk menunjukkan bahawa kami tidak menemui apa-apa. Anda sudah tahu bahawa carian binari memerlukan tatasusunan untuk diisih. Oleh itu, jika kita mempunyai tatasusunan yang tidak diisih di mana kita perlu mencari elemen tertentu, kita mempunyai dua pilihan:

1. Isih senarai dan gunakan carian binari
2. Pastikan senarai sentiasa diisih sambil menambah dan mengalih keluar elemen daripadanya secara serentak.

Satu cara untuk memastikan senarai diisih adalah dengan menggunakan pepohon carian binari. Pepohon carian binari ialah struktur data yang memenuhi keperluan berikut:

• Ia ialah pokok (struktur data yang meniru struktur pokok - ia mempunyai akar dan nod lain (daun) yang disambungkan oleh "dahan" atau tepi tanpa kitaran)
• Setiap nod mempunyai 0, 1 atau 2 anak
• Kedua-dua subpokok kiri dan kanan ialah pokok carian binari.
• Semua nod subpokok kiri nod X sewenang-wenangnya mempunyai nilai kunci data kurang daripada nilai kunci data nod X itu sendiri.
• Semua nod dalam subpokok kanan nod X sewenang-wenangnya mempunyai nilai kunci data yang lebih besar daripada atau sama dengan nilai kunci data nod X itu sendiri.

Perhatian: akar pokok "programmer", tidak seperti yang sebenar, berada di bahagian atas. Setiap sel dipanggil bucu, dan bucu disambungkan dengan tepi. Akar pokok ialah nombor sel 13. Subpokok kiri puncak 3 diserlahkan dalam warna dalam gambar di bawah: 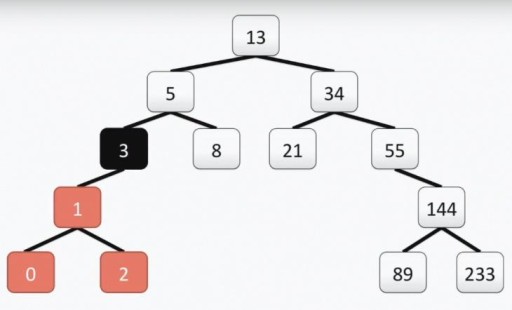Pokok kami memenuhi semua keperluan untuk pokok binari. Ini bermakna setiap subpokok kirinya hanya mengandungi nilai yang kurang daripada atau sama dengan nilai bucu, manakala subpokok kanan hanya mengandungi nilai yang lebih besar daripada atau sama dengan nilai bucu. Kedua-dua subpokok kiri dan kanan adalah subpokok binari sendiri. Kaedah membina pokok binari bukan satu-satunya: di bawah dalam gambar anda melihat pilihan lain untuk set nombor yang sama, dan mungkin terdapat banyak daripada mereka dalam amalan. Struktur ini membantu untuk menjalankan carian: kami mencari nilai minimum dengan bergerak dari atas ke kiri dan ke bawah setiap kali. 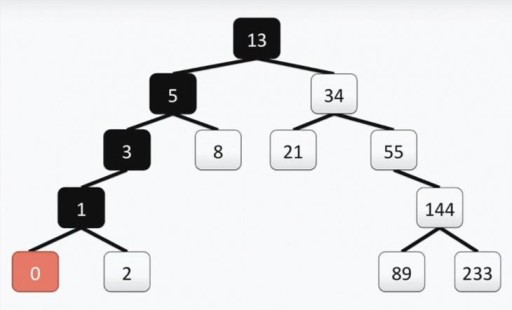Jika anda perlu mencari nombor maksimum, kami pergi dari atas ke bawah dan ke kanan. Mencari nombor yang bukan minimum atau maksimum juga agak mudah. Kami turun dari akar ke kiri atau ke kanan, bergantung pada sama ada puncak kami lebih besar atau lebih kecil daripada yang kami cari. Jadi, jika kita perlu mencari nombor 89, kita melalui laluan ini: Anda juga boleh memaparkan nombor dalam susunan pengisihan. Sebagai contoh, jika kita perlu memaparkan semua nombor dalam tertib menaik, kita mengambil subpokok kiri dan, bermula dari puncak paling kiri, naik. Menambah sesuatu pada pokok itu juga mudah. Perkara utama yang perlu diingat ialah struktur. Katakan kita perlu menambah nilai 7 pada pokok. Mari pergi ke akar dan semak. Nombor 7 < 13, jadi kita pergi ke kiri. Kami melihat 5 di sana, dan kami pergi ke kanan, sejak 7 > 5. Selanjutnya, kerana 7 > 8 dan 8 tidak mempunyai keturunan, kami membina cawangan dari 8 ke kiri dan melekatkan 7 padanya. Anda juga boleh mengeluarkan bucu dari pokok, tetapi ini agak rumit. Terdapat tiga senario pemadaman berbeza yang perlu kita pertimbangkan.

1. Pilihan paling mudah: kita perlu memadamkan bucu yang tidak mempunyai anak. Contohnya, nombor 7 yang baru kita tambah. Dalam kes ini, kami hanya mengikut laluan ke puncak dengan nombor ini dan memadamkannya.
2. Sebuah bucu mempunyai satu bucu anak. Dalam kes ini, anda boleh memadamkan puncak yang dikehendaki, tetapi keturunannya mesti disambungkan kepada "datuk", iaitu, puncak dari mana moyang terdekatnya berkembang. Sebagai contoh, dari pokok yang sama kita perlu mengeluarkan nombor 3. Dalam kes ini, kita bergabung dengan keturunannya, satu, bersama-sama dengan keseluruhan subpokok kepada 5. Ini dilakukan secara ringkas, kerana semua bucu di sebelah kiri 5 akan menjadi kurang daripada nombor ini (dan kurang daripada triple jauh).
3. Kes yang paling sukar ialah apabila puncak yang dipadamkan mempunyai dua anak. Sekarang perkara pertama yang perlu kita lakukan ialah mencari bucu di mana nilai yang lebih besar seterusnya disembunyikan, kita perlu menukarnya, dan kemudian memadamkan bucu yang dikehendaki. Ambil perhatian bahawa puncak nilai tertinggi seterusnya tidak boleh mempunyai dua anak, maka anak kirinya akan menjadi calon terbaik untuk nilai seterusnya. Mari kita keluarkan nod akar 13 daripada pokok kita. Mula-mula, kita cari nombor yang paling hampir dengan 13, yang lebih besar daripadanya. Ini ialah 21. Tukar 21 dan 13 dan padamkan 13.

Terdapat pelbagai cara untuk membina pokok binari, ada yang baik, yang lain tidak begitu baik. Apa yang berlaku jika kita cuba membina pokok binari daripada senarai yang disusun? Semua nombor hanya akan ditambah ke cawangan kanan yang sebelumnya. Jika kita ingin mencari nombor, kita tidak akan mempunyai pilihan selain hanya mengikuti rantai ke bawah. Ia tidak lebih baik daripada carian linear. Terdapat struktur data lain yang lebih kompleks. Tetapi kami tidak akan mempertimbangkan mereka buat masa ini. Katakan sahaja bahawa untuk menyelesaikan masalah membina pokok daripada senarai diisih, anda boleh mencampurkan data input secara rawak.

Isih algoritma

Terdapat susunan nombor. Kita perlu menyusunnya. Untuk kesederhanaan, kami akan menganggap bahawa kami mengisih integer dalam tertib menaik (dari terkecil kepada terbesar). Terdapat beberapa cara yang diketahui untuk mencapai proses ini. Selain itu, anda sentiasa boleh memimpikan topik dan menghasilkan pengubahsuaian algoritma.

Isih mengikut pilihan

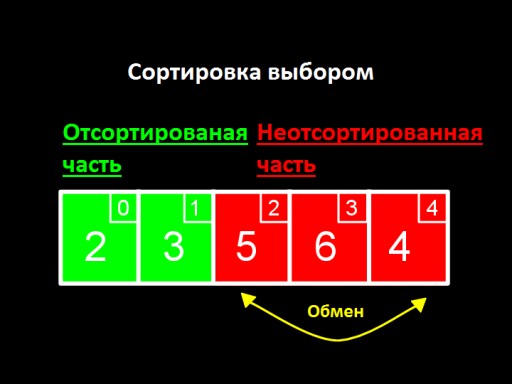Idea utama adalah untuk membahagikan senarai kami kepada dua bahagian, diisih dan tidak diisih. Pada setiap langkah algoritma, nombor baharu dialihkan dari bahagian yang tidak diisih ke bahagian yang diisih, dan seterusnya sehingga semua nombor berada di bahagian yang diisih.

1. Cari nilai minimum yang tidak diisih.
2. Kami menukar nilai ini dengan nilai pertama yang tidak diisih, dengan itu meletakkannya pada penghujung tatasusunan yang diisih.
3. Jika masih ada nilai yang tidak diisih, kembali ke langkah 1.

Pada langkah pertama, semua nilai tidak diisih. Mari kita panggil bahagian yang tidak diisih Unsorted, dan bahagian yang diisih Diisih (ini hanyalah perkataan Inggeris, dan kami melakukan ini hanya kerana Sorted adalah lebih pendek daripada "Bahagian yang diisih" dan akan kelihatan lebih baik dalam gambar). Kami mencari nombor minimum dalam bahagian tatasusunan yang tidak diisih (iaitu, pada langkah ini - dalam keseluruhan tatasusunan). Nombor ini ialah 2. Sekarang kita menukarnya dengan yang pertama antara yang belum diisih dan meletakkannya di penghujung tatasusunan yang diisih (pada langkah ini - di tempat pertama). Dalam langkah ini, ini ialah nombor pertama dalam tatasusunan, iaitu, 3. Langkah kedua. Kami tidak melihat nombor 2; ia sudah berada dalam subbaris yang diisih. Kami mula mencari minimum, bermula dari elemen kedua, ini adalah 5. Kami memastikan bahawa 3 adalah minimum antara yang tidak diisih, 5 adalah yang pertama di kalangan yang tidak diisih. Kami menukarnya dan menambah 3 pada subarray yang diisih. Dalam langkah ketiga , kita melihat bahawa nombor terkecil dalam subarray yang tidak diisih ialah 4. Kami menukarnya dengan nombor pertama antara yang tidak diisih - 5. Dalam langkah keempat, kita dapati bahawa dalam tatasusunan yang tidak diisih nombor terkecil ialah 5. Kami menukarnya daripada 6 dan menambahnya pada subarray yang diisih . 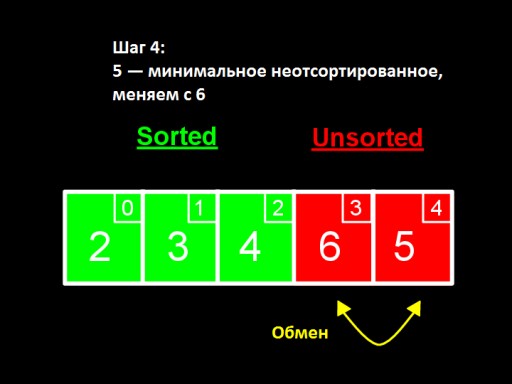Apabila hanya satu nombor kekal antara yang tidak diisih (yang terbesar), ini bermakna keseluruhan tatasusunan diisih! 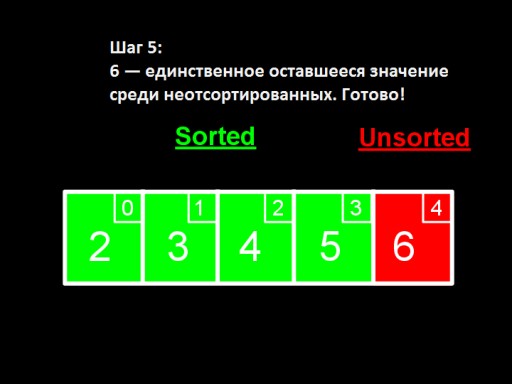Inilah rupa pelaksanaan tatasusunan dalam kod. Cuba buat sendiri. Dalam kedua-dua kes terbaik dan terburuk, untuk mencari elemen tidak diisih minimum, kita mesti membandingkan setiap elemen dengan setiap elemen tatasusunan yang tidak diisih, dan kita akan melakukan ini pada setiap lelaran. Tetapi kita tidak perlu melihat keseluruhan senarai, tetapi hanya bahagian yang tidak diisih. Adakah ini mengubah kelajuan algoritma? Dalam langkah pertama, untuk tatasusunan 5 elemen, kita membuat 4 perbandingan, dalam kedua - 3, dalam ketiga - 2. Untuk mendapatkan bilangan perbandingan, kita perlu menambah semua nombor ini. Kami mendapat jumlah Oleh itu, kelajuan dijangka algoritma dalam kes terbaik dan terburuk ialah Θ(n ² ). Bukan algoritma yang paling berkesan! Walau bagaimanapun, untuk tujuan pendidikan dan untuk set data kecil ia agak terpakai.

Isih gelembung

Algoritma isihan gelembung adalah salah satu yang paling mudah. Kami pergi bersama keseluruhan tatasusunan dan membandingkan 2 elemen jiran. Jika mereka dalam susunan yang salah, kami menukarnya. Pada hantaran pertama, elemen terkecil akan muncul ("terapung") pada penghujung (jika kita mengisih dalam tertib menurun). Ulangi langkah pertama jika sekurang-kurangnya satu pertukaran telah selesai dalam langkah sebelumnya. Mari kita susun tatasusunan. Langkah 1: pergi melalui tatasusunan. Algoritma bermula dengan dua elemen pertama, 8 dan 6, dan menyemak untuk melihat sama ada ia berada dalam susunan yang betul. 8 > 6, jadi kami menukarnya. Seterusnya kita melihat elemen kedua dan ketiga, kini ini adalah 8 dan 4. Atas sebab yang sama, kita menukarnya. Untuk kali ketiga kita membandingkan 8 dan 2. Secara keseluruhan, kita membuat tiga pertukaran (8, 6), (8, 4), (8, 2). Nilai 8 "terapung" ke penghujung senarai dalam kedudukan yang betul. Langkah 2: tukar (6,4) dan (6,2). 6 kini berada di kedudukan kedua terakhir, dan tidak perlu membandingkannya dengan "ekor" senarai yang telah disusun. Langkah 3: tukar 4 dan 2. Empat "terapung" ke tempat yang sepatutnya. Langkah 4: kita melalui tatasusunan, tetapi kita tiada apa-apa untuk diubah. Ini menandakan bahawa tatasusunan telah diisih sepenuhnya. 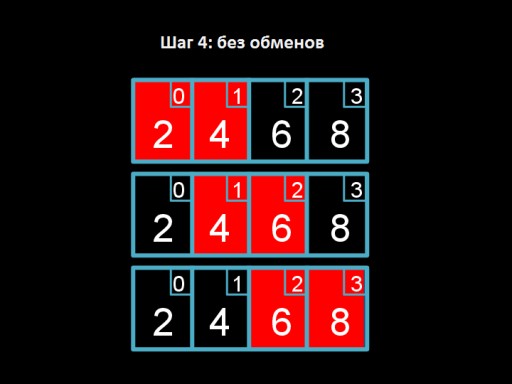Dan ini adalah kod algoritma. Cuba laksanakan dalam C! Isih gelembung mengambil masa O(n ² ) dalam kes yang paling teruk (semua nombor adalah salah), kerana kita perlu mengambil n langkah pada setiap lelaran, yang mana terdapat juga n. Malah, seperti dalam kes algoritma isihan pemilihan, masa akan menjadi kurang sedikit (n ² /2 – n/2), tetapi ini boleh diabaikan. Dalam kes terbaik (jika semua elemen sudah ada), kita boleh melakukannya dalam n langkah, i.e. Ω(n), kerana kita hanya perlu mengulangi tatasusunan sekali dan pastikan semua elemen berada di tempatnya (iaitu elemen n-1).

Isihan sisipan

Idea utama algoritma ini adalah untuk membahagikan tatasusunan kami kepada dua bahagian, diisih dan tidak diisih. Pada setiap langkah algoritma, nombor bergerak dari bahagian yang tidak diisih ke bahagian yang diisih. Mari lihat cara isihan sisipan berfungsi menggunakan contoh di bawah. Sebelum kita mula, semua elemen dianggap tidak diisih. Langkah 1: Ambil nilai pertama yang tidak diisih (3) dan masukkannya ke dalam subarray yang diisih. Pada langkah ini, keseluruhan subbaris yang diisih, permulaan dan penghujungnya akan menjadi tiga ini. Langkah 2: Sejak 3 > 5, kami akan memasukkan 5 ke dalam subarray yang diisih di sebelah kanan 3. Langkah 3: Sekarang kami berusaha untuk memasukkan nombor 2 ke dalam tatasusunan kami yang diisih. Kami membandingkan 2 dengan nilai dari kanan ke kiri untuk mencari kedudukan yang betul. Sejak 2 < 5 dan 2 < 3 dan kami telah mencapai permulaan subarray yang diisih. Oleh itu, kita mesti memasukkan 2 ke kiri 3. Untuk melakukan ini, gerakkan 3 dan 5 ke kanan supaya terdapat ruang untuk 2 dan masukkannya pada permulaan tatasusunan. Langkah 4. Kami bernasib baik: 6 > 5, jadi kami boleh memasukkan nombor itu sejurus selepas nombor 5. Langkah 5. 4 < 6 dan 4 < 5, tetapi 4 > 3. Oleh itu, kami tahu bahawa 4 mesti dimasukkan ke hak 3. Sekali lagi, kami terpaksa bergerak 5 dan 6 ke kanan untuk mencipta jurang untuk 4. Selesai! Algoritma Umum: Ambil setiap elemen yang tidak diisih bagi n dan bandingkan dengan nilai dalam subarray yang diisih dari kanan ke kiri sehingga kita menemui kedudukan yang sesuai untuk n (iaitu, saat kita mencari nombor pertama yang kurang daripada n) . Kemudian kami mengalihkan semua elemen yang diisih yang berada di sebelah kanan nombor ini ke kanan untuk memberi ruang kepada n kami, dan kami memasukkannya ke sana, dengan itu mengembangkan bahagian yang diisih tatasusunan. Untuk setiap elemen yang tidak diisih n anda perlukan:

2. Tentukan lokasi dalam bahagian disusun tatasusunan di mana n harus disisipkan
3. Alihkan elemen yang diisih ke kanan untuk mencipta jurang bagi n
4. Masukkan n ke dalam jurang yang terhasil dalam bahagian disusun tatasusunan.

Dan inilah kodnya! Kami mengesyorkan anda menulis versi program pengisihan anda sendiri.

Kelajuan asimptotik algoritma

Dalam kes yang paling teruk, kami akan membuat satu perbandingan dengan elemen kedua, dua perbandingan dengan yang ketiga, dan seterusnya. Oleh itu kelajuan kita ialah O(n ² ). Paling baik, kami akan bekerja dengan tatasusunan yang telah diisih. Bahagian yang disusun, yang kita bina dari kiri ke kanan tanpa sisipan dan pergerakan unsur, akan mengambil masa Ω(n).

Gabungkan jenis

Algoritma ini adalah rekursif; ia memecahkan satu masalah pengisihan besar kepada subtugas, pelaksanaannya menjadikannya lebih dekat untuk menyelesaikan masalah besar asal. Idea utama adalah untuk memisahkan tatasusunan yang tidak diisih kepada dua bahagian dan menyusun bahagian individu secara rekursif. Katakan kita mempunyai n elemen untuk diisih. Jika n < 2, kita selesai menyusun, jika tidak, kita mengisih bahagian kiri dan kanan tatasusunan secara berasingan, dan kemudian menggabungkannya. Mari kita susun tatasusunan. Bahagikannya kepada dua bahagian, dan teruskan bahagi sehingga kita mendapat subarray bersaiz 1, yang jelas disusun. Dua subarray yang diisih boleh digabungkan dalam masa O(n) menggunakan algoritma mudah: alih keluar nombor yang lebih kecil pada permulaan setiap subarray dan masukkannya ke dalam tatasusunan yang digabungkan. Ulang sehingga semua elemen hilang. Isih gabungan mengambil masa O(nlog n) untuk semua kes. Semasa kami membahagikan tatasusunan kepada separuh pada setiap tahap rekursi kami mendapat log n. Kemudian, menggabungkan subarray hanya memerlukan n perbandingan. Oleh itu O(nlog n). Kes terbaik dan terburuk untuk isihan gabungan adalah sama, jangkaan masa berjalan algoritma = Θ(nlog n). Algoritma ini adalah yang paling berkesan di kalangan mereka yang dipertimbangkan.