Mierzenie szybkości algorytmu w czasie rzeczywistym – w sekundach i minutach – nie jest łatwe. Jeden program może działać wolniej od drugiego nie z powodu własnej nieefektywności, ale z powodu powolności systemu operacyjnego, niezgodności ze sprzętem, zajmowania pamięci komputera przez inne procesy... Aby zmierzyć skuteczność algorytmów, wymyślono uniwersalne koncepcje niezależnie od środowiska, w którym program jest uruchomiony. Asymptotyczną złożoność problemu mierzy się za pomocą notacji Big O. Niech f(x) i g(x) będą funkcjami zdefiniowanymi w pewnym sąsiedztwie x0 i g tam nie znika. Wtedy f jest „O” większe niż g dla (x -> x0) jeśli istnieje stała C> 0 , że dla wszystkich x z pewnego otoczenia punktu x0 zachodzi nierówność |f(x)| <= C |g(x)| Nieco mniej rygorystyczna: f jest „O” większe niż g jeśli istnieje stała C>0, co dla wszystkich x > x0 f(x) <= C*g(x) Nie bój się formalna definicja! Zasadniczo określa asymptotyczny wzrost czasu działania programu, gdy ilość danych wejściowych rośnie w kierunku nieskończoności. Na przykład porównujesz sortowanie tablicy składającej się z 1000 i 10 elementów i musisz zrozumieć, jak wydłuży się czas działania programu. Lub musisz obliczyć długość ciągu znaków, przechodząc znak po znaku i dodając 1 dla każdego znaku: c - 1 a - 2 t - 3 Jego prędkość asymptotyczna = O(n), gdzie n to liczba liter w słowie. Jeśli liczysz według tej zasady, czas potrzebny na przeliczenie całej linii jest proporcjonalny do ilości znaków. Zliczanie znaków w ciągu 20-znakowym zajmuje dwa razy więcej czasu niż liczenie znaków w ciągu 10-znakowym. Wyobraź sobie, że w zmiennej długości zapisałeś wartość równą liczbie znaków w ciągu. Na przykład długość = 1000. Aby poznać długość łańcucha wystarczy dostęp do tej zmiennej, nie trzeba nawet patrzeć na sam ciąg. I niezależnie od tego, jak zmienimy długość, zawsze mamy dostęp do tej zmiennej. W tym przypadku prędkość asymptotyczna = O(1). Zmiana danych wejściowych nie zmienia szybkości takiego zadania, wyszukiwanie odbywa się w stałym czasie. W tym przypadku program jest asymptotycznie stały. Wada: marnujesz pamięć komputera na przechowywanie dodatkowej zmiennej i dodatkowy czas na aktualizację jej wartości. Jeśli uważasz, że czas liniowy jest zły, zapewniamy, że może być znacznie gorszy. Na przykład O(n 2 ). Zapis ten oznacza, że wraz ze wzrostem n czas wymagany do iteracji przez elementy (lub inną akcję) będzie rósł coraz gwałtowniej. Jednak dla małego n algorytmy o prędkości asymptotycznej O(n 2 ) mogą działać szybciej niż algorytmy o prędkości asymptotycznej O(n). Ale w pewnym momencie funkcja kwadratowa wyprzedzi funkcję liniową, nie da się tego obejść. Inną złożonością asymptotyczną jest czas logarytmiczny lub O (log n). Wraz ze wzrostem n funkcja ta rośnie bardzo powoli. O(log n) to czas działania klasycznego algorytmu wyszukiwania binarnego w posortowanej tablicy (pamiętasz podartą książkę telefoniczną na wykładzie?). Tablicę dzielimy na dwie części, następnie wybieramy połowę, w której znajduje się element, i tak za każdym razem zmniejszając obszar poszukiwań o połowę, szukamy elementu. Co się stanie, jeśli od razu natkniemy się na to, czego szukamy, dzieląc po raz pierwszy naszą tablicę danych na pół? Istnieje określenie najlepszego czasu – Omega-large lub Ω(n). W przypadku wyszukiwania binarnego = Ω(1) (znalezienie w czasie stałym, niezależnie od wielkości tablicy). Wyszukiwanie liniowe przebiega w czasie O(n) i Ω(1), jeżeli szukany element jest pierwszym. Innym symbolem jest theta (Θ(n)). Stosuje się go, gdy najlepsze i najgorsze opcje są takie same. Jest to odpowiednie w przykładzie, w którym długość ciągu znaków przechowywaliśmy w osobnej zmiennej, więc dla dowolnej długości wystarczy odwołać się do tej zmiennej. W przypadku tego algorytmu najlepszym i najgorszym przypadkiem są odpowiednio Ω(1) i O(1). Oznacza to, że algorytm działa w czasie Θ(1).
Wyszukiwanie liniowe
Otwierając przeglądarkę internetową, szukając strony, informacji, znajomych na portalach społecznościowych, dokonujesz wyszukiwania, zupełnie tak samo, jak próbując znaleźć odpowiednią parę butów w sklepie. Zapewne zauważyłeś, że porządek ma duży wpływ na sposób wyszukiwania. Jeśli masz w szafie wszystkie koszule, zazwyczaj łatwiej jest znaleźć wśród nich tę, której potrzebujesz, niż wśród tych rozrzuconych bez systemu po całym pomieszczeniu. Wyszukiwanie liniowe to metoda wyszukiwania sekwencyjnego, jeden po drugim. Przeglądając wyniki wyszukiwania Google od góry do dołu, korzystasz z wyszukiwania liniowego. Przykład . Powiedzmy, że mamy listę liczb: 2 4 0 5 3 7 8 1 I musimy znaleźć 0. Widzimy to od razu, ale program komputerowy nie działa w ten sposób. Zaczyna od początku listy i widzi cyfrę 2. Następnie sprawdza: 2=0? Tak nie jest, więc kontynuuje i przechodzi do drugiej postaci. Tam też czeka ją porażka i dopiero na trzeciej pozycji algorytm znajduje wymaganą liczbę. Pseudokod wyszukiwania liniowego: Funkcja linearSearch otrzymuje na wejściu dwa argumenty - klucz klucz i tablicę array[.Kluczem jest żądana wartość, w poprzednim przykładzie klucz = 0. Tablica jest listą liczb, które możemy przejrzę. Jeśli nic nie znaleźliśmy, funkcja zwróci -1 (pozycja, która nie istnieje w tablicy). Jeśli wyszukiwanie liniowe znajdzie żądany element, funkcja zwróci pozycję, w której znajduje się żądany element w tablicy. Zaletą wyszukiwania liniowego jest to, że będzie działać dla dowolnej tablicy, niezależnie od kolejności elementów: nadal będziemy przeglądać całą tablicę. To jest także jego słabość. Jeśli chcesz znaleźć liczbę 198 w tablicy 200 liczb posortowanych w odpowiedniej kolejności, pętla for wykona 198 kroków. Prawdopodobnie już zgadłeś, która metoda działa lepiej w przypadku posortowanej tablicy?
Wyszukiwanie binarne i drzewa
Wyobraź sobie, że masz listę postaci Disneya posortowaną alfabetycznie i musisz znaleźć Myszkę Miki. Liniowo zajęłoby to dużo czasu. A jeśli zastosujemy „metodę rozdzierania katalogu na pół”, to trafimy od razu do Jasmine i będziemy mogli bezpiecznie odrzucić pierwszą połowę listy, mając świadomość, że Mickeya tam nie może być. Stosując tę samą zasadę, odrzucamy drugą kolumnę. Kontynuując tę strategię, w kilku krokach odnajdziemy Mickeya. Znajdźmy liczbę 144. Dzielimy listę na pół i dochodzimy do liczby 13. Oceniamy, czy szukana liczba jest większa czy mniejsza od 13. 13 < 144, więc możemy zignorować wszystko po lewej stronie 13 i sama ta liczba. Teraz nasza lista wyszukiwania wygląda tak: 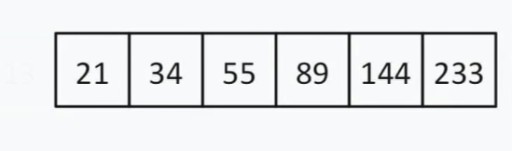Elementów jest parzysta, więc wybieramy zasadę według której wybieramy „środek” (bliżej początku lub końca). Powiedzmy, że wybraliśmy strategię bliskości początku. W tym przypadku nasz „środek” = 55. 55 < 144. Ponownie odrzucamy lewą połowę listy. Na szczęście dla nas następna średnia liczba to 144. Znaleźliśmy 144 w 13-elementowej tablicy, korzystając z wyszukiwania binarnego w zaledwie trzech krokach. Wyszukiwanie liniowe poradziłoby sobie z tą samą sytuacją w aż 12 krokach. Ponieważ algorytm ten w każdym kroku zmniejsza liczbę elementów tablicy o połowę, znajdzie wymagany element w czasie asymptotycznym O(log n), gdzie n jest liczbą elementów na liście. Oznacza to, że w naszym przypadku czas asymptotyczny = O(log 13) (to trochę więcej niż trzy). Pseudokod funkcji wyszukiwania binarnego: 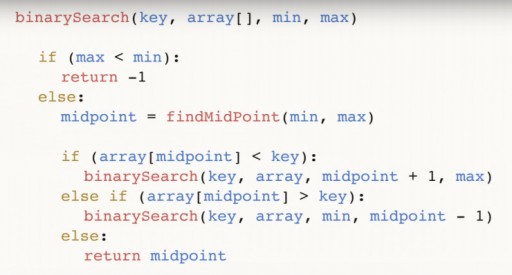Funkcja przyjmuje na wejściu 4 argumenty: żądany klucz, tablicę danych tablica [], w której znajduje się żądana, min i max są wskaźnikami do maksymalnej i minimalnej liczby w tablicy, które patrzymy na ten etap algorytmu. Dla naszego przykładu początkowo podano następujący obrazek: Przeanalizujmy kod dalej. punkt środkowy jest naszym środkiem tablicy. Zależy od skrajnych punktów i jest wyśrodkowany pomiędzy nimi. Po znalezieniu środka sprawdzamy, czy jest on mniejszy od naszej liczby klucza. Jeśli tak, to klucz jest również większy od którejkolwiek z liczb na lewo od środka i możemy ponownie wywołać funkcję binarną, tylko teraz, że nasz min = punkt środkowy + 1. Jeśli okaże się, że klucz < punkt środkowy, możemy odrzucić ten numer i wszystkie liczby , leżące po jego prawej stronie. I wywołujemy przeszukiwanie binarne tablicy od liczby min do wartości (punkt środkowy – 1). Wreszcie trzecia gałąź: jeśli wartość w punkcie środkowym nie jest ani większa, ani mniejsza od klucza, nie ma innego wyjścia, jak tylko być żądaną liczbą. W takim przypadku zwracamy go i kończymy program. Wreszcie może się zdarzyć, że szukanej liczby w ogóle nie ma w tablicy. Aby uwzględnić ten przypadek, przeprowadzamy następującą kontrolę: I zwracamy (-1), aby wskazać, że niczego nie znaleźliśmy. Wiesz już, że wyszukiwanie binarne wymaga posortowania tablicy. Zatem jeśli mamy nieposortowaną tablicę, w której musimy znaleźć określony element, mamy dwie możliwości:
Posortuj listę i zastosuj wyszukiwanie binarne
Utrzymuj listę zawsze posortowaną, jednocześnie dodając i usuwając z niej elementy.
Jednym ze sposobów uporządkowania list jest użycie drzewa wyszukiwania binarnego. Drzewo wyszukiwania binarnego to struktura danych spełniająca następujące wymagania:
Jest to drzewo (struktura danych emulująca strukturę drzewa - ma korzeń i inne węzły (liście) połączone „gałęziami” lub krawędziami bez cykli)
Każdy węzeł ma 0, 1 lub 2 dzieci
Zarówno lewe, jak i prawe poddrzewo są drzewami wyszukiwania binarnego.
Wszystkie węzły lewego poddrzewa dowolnego węzła X mają wartości klucza danych mniejsze niż wartość klucza danych samego węzła X.
Wszystkie węzły w prawym poddrzewie dowolnego węzła X mają wartości klucza danych większe lub równe wartości klucza danych samego węzła X.
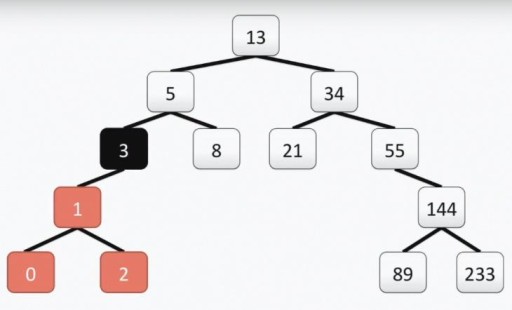Uwaga: korzeń drzewa „programisty”, w przeciwieństwie do prawdziwego, znajduje się na górze. Każda komórka nazywana jest wierzchołkiem, a wierzchołki są połączone krawędziami. Korzeń drzewa to komórka numer 13. Lewe poddrzewo wierzchołka 3 zostało zaznaczone kolorem na poniższym obrazku: Nasze drzewo spełnia wszystkie wymagania dla drzew binarnych. Oznacza to, że każde z jego lewych poddrzew zawiera tylko wartości mniejsze lub równe wartości wierzchołka, natomiast prawe poddrzewo zawiera tylko wartości większe lub równe wartości wierzchołka. Zarówno lewe, jak i prawe poddrzewo same w sobie są poddrzewami binarnymi. Sposób konstruowania drzewa binarnego nie jest jedyny: poniżej na obrazku widać inną opcję dla tego samego zestawu liczb, a w praktyce może być ich dużo. Ta struktura pomaga w przeszukiwaniu: wartość minimalną znajdujemy przesuwając się za każdym razem od góry do lewej i w dół. 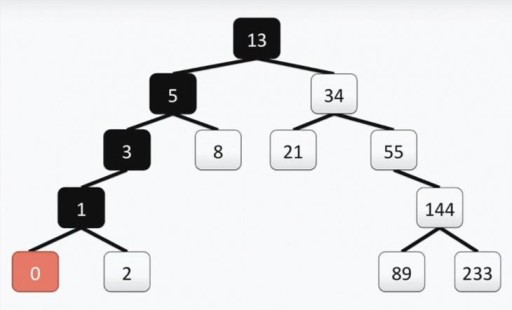Jeśli chcesz znaleźć maksymalną liczbę, idziemy od góry do dołu i w prawo. Znalezienie liczby, która nie jest minimalną lub maksymalną liczbą, jest również dość proste. Od korzenia schodzimy w lewo lub w prawo, w zależności od tego, czy nasz wierzchołek jest większy, czy mniejszy od tego, którego szukamy. Jeśli więc musimy znaleźć liczbę 89, postępujemy następującą ścieżką: Możesz także wyświetlić liczby w kolejności sortowania. Na przykład, jeśli chcemy wyświetlić wszystkie liczby w kolejności rosnącej, bierzemy lewe poddrzewo i zaczynając od lewego wierzchołka, idziemy w górę. Dodanie czegoś do drzewa jest również łatwe. Najważniejszą rzeczą do zapamiętania jest struktura. Powiedzmy, że musimy dodać do drzewa wartość 7. Przejdźmy do korzenia i sprawdźmy. Liczba 7 < 13, więc idziemy w lewo. Widzimy tam 5 i idziemy w prawo, ponieważ 7 > 5. Ponadto, ponieważ 7 > 8 i 8 nie ma potomków, konstruujemy gałąź od 8 w lewo i dołączamy do niej 7. Możesz także usunąć wierzchołki z drzewo, ale jest to nieco bardziej skomplikowane. Istnieją trzy różne scenariusze usuwania, które musimy rozważyć.
Najprostsza opcja: musimy usunąć wierzchołek, który nie ma dzieci. Na przykład liczba 7, którą właśnie dodaliśmy. W tym przypadku po prostu podążamy ścieżką do wierzchołka z tym numerem i usuwamy go.
Wierzchołek ma jeden wierzchołek potomny. W takim przypadku możesz usunąć żądany wierzchołek, ale jego potomek musi być połączony z „dziadkiem”, czyli wierzchołkiem, z którego wyrósł jego bezpośredni przodek. Na przykład z tego samego drzewa musimy usunąć liczbę 3. W tym przypadku łączymy jej potomka, jeden, wraz z całym poddrzewem do liczby 5. Robi się to po prostu, ponieważ wszystkie wierzchołki na lewo od liczby 5 zostaną mniej niż ta liczba (i mniej niż odległa potrójna liczba).
Najtrudniejszy przypadek ma miejsce, gdy usuwany wierzchołek ma dwójkę dzieci. Teraz pierwszą rzeczą, którą musimy zrobić, to znaleźć wierzchołek, w którym ukryta jest kolejna większa wartość, musimy je zamienić, a następnie usunąć żądany wierzchołek. Należy pamiętać, że kolejny wierzchołek o najwyższej wartości nie może mieć dwójki dzieci, wówczas jego lewe dziecko będzie najlepszym kandydatem na następną wartość. Usuńmy z naszego drzewa węzeł główny 13. Najpierw szukamy liczby najbliższej 13, która jest od niej większa. To jest 21. Zamień 21 z 13 i usuń 13.
Istnieją różne sposoby budowania drzew binarnych, niektóre dobre, inne niezbyt dobre. Co się stanie, jeśli spróbujemy zbudować drzewo binarne z posortowanej listy? Wszystkie liczby zostaną po prostu dodane do prawej gałęzi poprzedniej. Jeśli chcemy znaleźć liczbę, nie będziemy mieli innego wyjścia, jak po prostu podążać za łańcuchem w dół. Nie jest to lepsze niż wyszukiwanie liniowe. Istnieją inne struktury danych, które są bardziej złożone. Ale na razie nie będziemy ich rozważać. Powiedzmy, że aby rozwiązać problem konstruowania drzewa z posortowanej listy, możesz losowo mieszać dane wejściowe.
Algorytmy sortowania
Istnieje tablica liczb. Musimy to uporządkować. Dla uproszczenia założymy, że sortujemy liczby całkowite w porządku rosnącym (od najmniejszej do największej). Istnieje kilka znanych sposobów przeprowadzenia tego procesu. Poza tym zawsze możesz wymyślić temat i zaproponować modyfikację algorytmu.
Sortowanie według wyboru
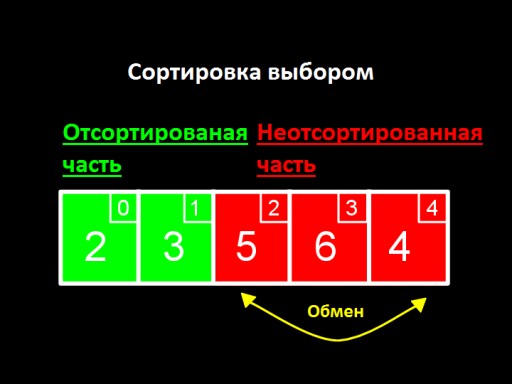Główną ideą jest podzielenie naszej listy na dwie części, posortowaną i nieposortowaną. Na każdym etapie algorytmu nowa liczba jest przenoszona z części nieposortowanej do części posortowanej i tak dalej, aż wszystkie liczby znajdą się w części posortowanej.
Znajdź minimalną nieposortowaną wartość.
Zamieniamy tę wartość z pierwszą nieposortowaną wartością, umieszczając ją w ten sposób na końcu posortowanej tablicy.
Jeśli pozostały nieposortowane wartości, wróć do kroku 1.
W pierwszym kroku wszystkie wartości są nieposortowane. Nazwijmy część nieposortowaną Unsorted, a część posortowaną Sorted (to tylko angielskie słowa i robimy to tylko dlatego, że Sorted jest znacznie krótsze niż „Posortowana część” i będzie lepiej wyglądać na zdjęciach). Minimalną liczbę znajdujemy w nieposortowanej części tablicy (czyli na tym etapie – w całej tablicy). Ta liczba to 2. Teraz zamieniamy ją na pierwszą spośród nieposortowanych i umieszczamy ją na końcu posortowanej tablicy (w tym kroku - na pierwszym miejscu). W tym kroku jest to pierwsza liczba w tablicy, czyli 3. Krok drugi. Nie patrzymy na liczbę 2; znajduje się ona już w posortowanej podtablicy. Zaczynamy szukać minimum zaczynając od drugiego elementu, czyli 5. Dbamy o to, aby 3 było minimum wśród nieposortowanych, 5 było pierwszym wśród nieposortowanych. Zamieniamy je i dodajemy 3 do posortowanej podtablicy. W trzecim kroku widzimy, że najmniejszą liczbą w nieposortowanej tablicy jest 4. Zamieniamy ją na pierwszą liczbę spośród nieposortowanych - 5. W czwartym kroku stwierdzamy, że w nieposortowanej tablicy najmniejszą liczbą jest 5. Zmieniamy go z 6 i dodajemy do posortowanej podtablicy. 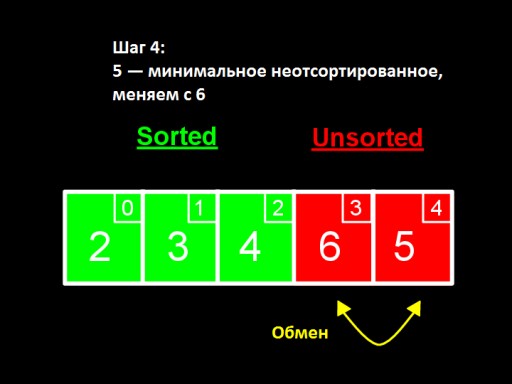Jeżeli wśród nieposortowanych (największych) pozostanie tylko jedna liczba, oznacza to, że cała tablica jest posortowana! 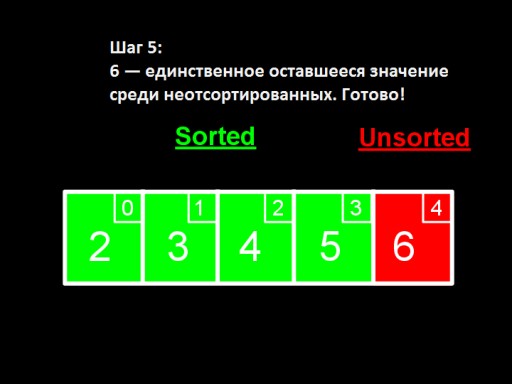Tak wygląda implementacja tablicy w kodzie. Spróbuj zrobić to sam. Zarówno w najlepszym, jak i najgorszym przypadku, aby znaleźć minimalny nieposortowany element, musimy porównać każdy element z każdym elementem nieposortowanej tablicy i będziemy to robić przy każdej iteracji. Ale nie musimy przeglądać całej listy, a jedynie nieposortowaną część. Czy zmienia to szybkość algorytmu? W pierwszym kroku dla tablicy składającej się z 5 elementów dokonujemy 4 porównań, w drugim - 3, w trzecim - 2. Aby otrzymać liczbę porównań należy wszystkie te liczby zsumować. Otrzymujemy sumę. Zatem oczekiwana prędkość algorytmu w najlepszym i najgorszym przypadku wynosi Θ(n 2 ). Nie jest to najbardziej wydajny algorytm! Jednak do celów edukacyjnych i dla małych zbiorów danych jest to całkiem przydatne.
Sortowanie bąbelkowe
Algorytm sortowania bąbelkowego jest jednym z najprostszych. Idziemy wzdłuż całej tablicy i porównujemy 2 sąsiednie elementy. Jeśli są w złej kolejności, zamieniamy je. Przy pierwszym przebiegu na końcu pojawi się najmniejszy element („float”) (jeśli sortujemy w kolejności malejącej). Powtórz pierwszy krok, jeśli w poprzednim kroku zakończono co najmniej jedną wymianę. Posortujmy tablicę. Krok 1: przejdź przez tablicę. Algorytm zaczyna od dwóch pierwszych elementów, 8 i 6, i sprawdza, czy są one ułożone we właściwej kolejności. 8 > 6, więc zamieniamy je. Następnie patrzymy na drugi i trzeci element, teraz są to 8 i 4. Z tych samych powodów zamieniamy je. Po raz trzeci porównujemy 8 i 2. W sumie dokonujemy trzech wymian (8, 6), (8, 4), (8, 2). Wartość 8 „przepłynęła” na koniec listy we właściwym miejscu. Krok 2: zamień (6,4) i (6,2). Numer 6 znajduje się teraz na przedostatniej pozycji i nie ma potrzeby porównywać go z już posortowanym „ogonem” listy. Krok 3: zamień 4 i 2. Czwórka „unosi się” na swoje właściwe miejsce. Krok 4: przeglądamy tablicę, ale nie mamy już nic do zmiany. Oznacza to, że tablica jest całkowicie posortowana. 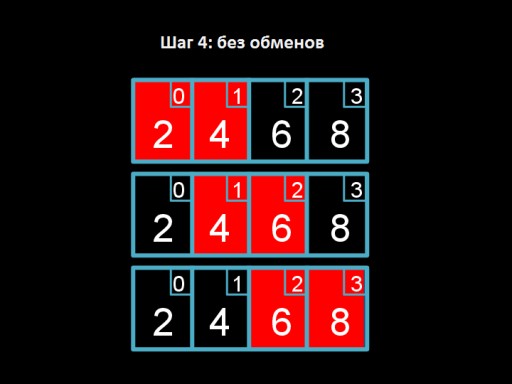A to jest kod algorytmu. Spróbuj zaimplementować to w C! Sortowanie bąbelkowe w najgorszym przypadku zajmuje O(n 2 ) czasu (wszystkie liczby są błędne), ponieważ w każdej iteracji musimy wykonać n kroków, których też jest n. Faktycznie, podobnie jak w przypadku algorytmu sortowania przez selekcję, czas będzie nieco krótszy (n 2 /2 – n/2), ale można to pominąć. W najlepszym przypadku (jeśli wszystkie elementy są już na swoim miejscu) możemy to zrobić w n krokach, tj. Ω(n), ponieważ będziemy musieli tylko raz wykonać iterację po tablicy i upewnić się, że wszystkie elementy są na swoich miejscach (tj. nawet elementy n-1).
Sortowanie przez wstawianie
Główną ideą tego algorytmu jest podzielenie naszej tablicy na dwie części, posortowaną i niesortowaną. Na każdym etapie algorytmu liczba przesuwa się od części nieposortowanej do posortowanej. Przyjrzyjmy się, jak działa sortowanie przez wstawianie, korzystając z poniższego przykładu. Zanim zaczniemy, wszystkie elementy uważa się za nieposortowane. Krok 1: Weź pierwszą nieposortowaną wartość (3) i wstaw ją do posortowanej podtablicy. Na tym etapie cała posortowana podtablica, jej początek i koniec będą wynosić właśnie te trzy. Krok 2: Ponieważ 3 > 5, wstawimy 5 do posortowanej podtablicy na prawo od 3. Krok 3: Teraz pracujemy nad wstawieniem liczby 2 do naszej posortowanej tablicy. Porównujemy 2 z wartościami od prawej do lewej, aby znaleźć właściwą pozycję. Ponieważ 2 < 5 i 2 < 3 i dotarliśmy do początku posortowanej podtablicy. Dlatego musimy wstawić 2 na lewo od 3. Aby to zrobić, przesuń 3 i 5 w prawo, aby było miejsce na 2 i wstaw je na początku tablicy. Krok 4. Mamy szczęście: 6 > 5, więc możemy wstawić tę liczbę zaraz po liczbie 5. Krok 5. 4 < 6 i 4 < 5, ale 4 > 3. Wiemy zatem, że do na prawo od 3. Ponownie jesteśmy zmuszeni przesunąć 5 i 6 w prawo, aby utworzyć lukę dla 4. Gotowe! Algorytm uogólniony: Weź każdy nieposortowany element n i porównaj go z wartościami w posortowanej podtablicy od prawej do lewej, aż znajdziemy odpowiednią pozycję dla n (to znaczy moment, w którym znajdziemy pierwszą liczbę mniejszą niż n) . Następnie przesuwamy wszystkie posortowane elementy znajdujące się na prawo od tej liczby w prawo, aby zrobić miejsce dla naszego n, i wstawiamy je tam, rozszerzając w ten sposób posortowaną część tablicy. Dla każdego nieposortowanego elementu n potrzebujesz:
Określ miejsce w posortowanej części tablicy, w którym należy wstawić n
Przesuń posortowane elementy w prawo, aby utworzyć przerwę dla n
Wstaw n w powstałą lukę w posortowanej części tablicy.
A oto kod! Zalecamy napisanie własnej wersji programu sortującego.
Asymptotyczna prędkość algorytmu
W najgorszym przypadku dokonamy jednego porównania z drugim elementem, dwa porównania z trzecim i tak dalej. Zatem nasza prędkość wynosi O(n 2 ). W najlepszym przypadku będziemy pracować z już posortowaną tablicą. Posortowana część, którą budujemy od lewej do prawej bez wstawiania i przesuwania elementów, zajmie czas Ω(n).
Sortowanie przez scalanie
Algorytm ten jest rekurencyjny; dzieli jeden duży problem sortowania na podzadania, których wykonanie przybliża rozwiązanie pierwotnego dużego problemu. Główną ideą jest podzielenie nieposortowanej tablicy na dwie części i rekursywne posortowanie poszczególnych połówek. Załóżmy, że mamy n elementów do posortowania. Jeśli n < 2, kończymy sortowanie, w przeciwnym razie sortujemy osobno lewą i prawą część tablicy, a następnie łączymy je. Posortujmy tablicę.Podzielmy ją na dwie części i kontynuujmy dzielenie, aż otrzymamy podtablice o rozmiarze 1, które są oczywiście posortowane. Dwie posortowane podtablice można połączyć w czasie O(n) za pomocą prostego algorytmu: usuń mniejszą liczbę z początku każdej podtablicy i wstaw ją do scalonej tablicy. Powtarzaj, aż znikną wszystkie elementy. Sortowanie przez scalanie zajmuje czas O(nlog n) dla wszystkich przypadków. Dzieląc tablice na połowy na każdym poziomie rekurencji, otrzymujemy log n. Następnie scalanie podtablic wymaga tylko n porównań. Zatem O(nlog n). Najlepsze i najgorsze przypadki sortowania przez scalanie są takie same, oczekiwany czas działania algorytmu = Θ(nlog n). Algorytm ten jest najskuteczniejszy spośród rozważanych.
Ale w pewnym momencie funkcja kwadratowa wyprzedzi funkcję liniową, nie da się tego obejść. Inną złożonością asymptotyczną jest czas logarytmiczny lub O (log n). Wraz ze wzrostem n funkcja ta rośnie bardzo powoli. O(log n) to czas działania klasycznego algorytmu wyszukiwania binarnego w posortowanej tablicy (pamiętasz podartą książkę telefoniczną na wykładzie?). Tablicę dzielimy na dwie części, następnie wybieramy połowę, w której znajduje się element, i tak za każdym razem zmniejszając obszar poszukiwań o połowę, szukamy elementu. 
Co się stanie, jeśli od razu natkniemy się na to, czego szukamy, dzieląc po raz pierwszy naszą tablicę danych na pół? Istnieje określenie najlepszego czasu – Omega-large lub Ω(n). W przypadku wyszukiwania binarnego = Ω(1) (znalezienie w czasie stałym, niezależnie od wielkości tablicy). Wyszukiwanie liniowe przebiega w czasie O(n) i Ω(1), jeżeli szukany element jest pierwszym. Innym symbolem jest theta (Θ(n)). Stosuje się go, gdy najlepsze i najgorsze opcje są takie same. Jest to odpowiednie w przykładzie, w którym długość ciągu znaków przechowywaliśmy w osobnej zmiennej, więc dla dowolnej długości wystarczy odwołać się do tej zmiennej. W przypadku tego algorytmu najlepszym i najgorszym przypadkiem są odpowiednio Ω(1) i O(1). Oznacza to, że algorytm działa w czasie Θ(1).
Funkcja linearSearch otrzymuje na wejściu dwa argumenty - klucz klucz i tablicę array[.Kluczem jest żądana wartość, w poprzednim przykładzie klucz = 0. Tablica jest listą liczb, które możemy przejrzę. Jeśli nic nie znaleźliśmy, funkcja zwróci -1 (pozycja, która nie istnieje w tablicy). Jeśli wyszukiwanie liniowe znajdzie żądany element, funkcja zwróci pozycję, w której znajduje się żądany element w tablicy. Zaletą wyszukiwania liniowego jest to, że będzie działać dla dowolnej tablicy, niezależnie od kolejności elementów: nadal będziemy przeglądać całą tablicę. To jest także jego słabość. Jeśli chcesz znaleźć liczbę 198 w tablicy 200 liczb posortowanych w odpowiedniej kolejności, pętla for wykona 198 kroków. 
Prawdopodobnie już zgadłeś, która metoda działa lepiej w przypadku posortowanej tablicy?
Liniowo zajęłoby to dużo czasu. A jeśli zastosujemy „metodę rozdzierania katalogu na pół”, to trafimy od razu do Jasmine i będziemy mogli bezpiecznie odrzucić pierwszą połowę listy, mając świadomość, że Mickeya tam nie może być. 
Stosując tę samą zasadę, odrzucamy drugą kolumnę. Kontynuując tę strategię, w kilku krokach odnajdziemy Mickeya. 
Znajdźmy liczbę 144. Dzielimy listę na pół i dochodzimy do liczby 13. Oceniamy, czy szukana liczba jest większa czy mniejsza od 13. 13 
< 144, więc możemy zignorować wszystko po lewej stronie 13 i sama ta liczba. Teraz nasza lista wyszukiwania wygląda tak: 
Elementów jest parzysta, więc wybieramy zasadę według której wybieramy „środek” (bliżej początku lub końca). Powiedzmy, że wybraliśmy strategię bliskości początku. W tym przypadku nasz „środek” = 55. 
55 < 144. Ponownie odrzucamy lewą połowę listy. Na szczęście dla nas następna średnia liczba to 144. 
Znaleźliśmy 144 w 13-elementowej tablicy, korzystając z wyszukiwania binarnego w zaledwie trzech krokach. Wyszukiwanie liniowe poradziłoby sobie z tą samą sytuacją w aż 12 krokach. Ponieważ algorytm ten w każdym kroku zmniejsza liczbę elementów tablicy o połowę, znajdzie wymagany element w czasie asymptotycznym O(log n), gdzie n jest liczbą elementów na liście. Oznacza to, że w naszym przypadku czas asymptotyczny = O(log 13) (to trochę więcej niż trzy). Pseudokod funkcji wyszukiwania binarnego: 
Funkcja przyjmuje na wejściu 4 argumenty: żądany klucz, tablicę danych tablica [], w której znajduje się żądana, min i max są wskaźnikami do maksymalnej i minimalnej liczby w tablicy, które patrzymy na ten etap algorytmu. Dla naszego przykładu początkowo podano następujący obrazek: 
Przeanalizujmy kod dalej. punkt środkowy jest naszym środkiem tablicy. Zależy od skrajnych punktów i jest wyśrodkowany pomiędzy nimi. Po znalezieniu środka sprawdzamy, czy jest on mniejszy od naszej liczby klucza. 
Jeśli tak, to klucz jest również większy od którejkolwiek z liczb na lewo od środka i możemy ponownie wywołać funkcję binarną, tylko teraz, że nasz min = punkt środkowy + 1. Jeśli okaże się, że klucz < punkt środkowy, możemy odrzucić ten numer i wszystkie liczby , leżące po jego prawej stronie. I wywołujemy przeszukiwanie binarne tablicy od liczby min do wartości (punkt środkowy – 1). 
Wreszcie trzecia gałąź: jeśli wartość w punkcie środkowym nie jest ani większa, ani mniejsza od klucza, nie ma innego wyjścia, jak tylko być żądaną liczbą. W takim przypadku zwracamy go i kończymy program. 
Wreszcie może się zdarzyć, że szukanej liczby w ogóle nie ma w tablicy. Aby uwzględnić ten przypadek, przeprowadzamy następującą kontrolę: 
I zwracamy (-1), aby wskazać, że niczego nie znaleźliśmy. Wiesz już, że wyszukiwanie binarne wymaga posortowania tablicy. Zatem jeśli mamy nieposortowaną tablicę, w której musimy znaleźć określony element, mamy dwie możliwości:
Uwaga: korzeń drzewa „programisty”, w przeciwieństwie do prawdziwego, znajduje się na górze. Każda komórka nazywana jest wierzchołkiem, a wierzchołki są połączone krawędziami. Korzeń drzewa to komórka numer 13. Lewe poddrzewo wierzchołka 3 zostało zaznaczone kolorem na poniższym obrazku: 
Nasze drzewo spełnia wszystkie wymagania dla drzew binarnych. Oznacza to, że każde z jego lewych poddrzew zawiera tylko wartości mniejsze lub równe wartości wierzchołka, natomiast prawe poddrzewo zawiera tylko wartości większe lub równe wartości wierzchołka. Zarówno lewe, jak i prawe poddrzewo same w sobie są poddrzewami binarnymi. Sposób konstruowania drzewa binarnego nie jest jedyny: poniżej na obrazku widać inną opcję dla tego samego zestawu liczb, a w praktyce może być ich dużo. 
Ta struktura pomaga w przeszukiwaniu: wartość minimalną znajdujemy przesuwając się za każdym razem od góry do lewej i w dół. 
Jeśli chcesz znaleźć maksymalną liczbę, idziemy od góry do dołu i w prawo. Znalezienie liczby, która nie jest minimalną lub maksymalną liczbą, jest również dość proste. Od korzenia schodzimy w lewo lub w prawo, w zależności od tego, czy nasz wierzchołek jest większy, czy mniejszy od tego, którego szukamy. Jeśli więc musimy znaleźć liczbę 89, postępujemy następującą ścieżką: 
Możesz także wyświetlić liczby w kolejności sortowania. Na przykład, jeśli chcemy wyświetlić wszystkie liczby w kolejności rosnącej, bierzemy lewe poddrzewo i zaczynając od lewego wierzchołka, idziemy w górę. Dodanie czegoś do drzewa jest również łatwe. Najważniejszą rzeczą do zapamiętania jest struktura. Powiedzmy, że musimy dodać do drzewa wartość 7. Przejdźmy do korzenia i sprawdźmy. Liczba 7 < 13, więc idziemy w lewo. Widzimy tam 5 i idziemy w prawo, ponieważ 7 > 5. Ponadto, ponieważ 7 > 8 i 8 nie ma potomków, konstruujemy gałąź od 8 w lewo i dołączamy do niej 7. Możesz także usunąć wierzchołki 
z drzewo, ale jest to nieco bardziej skomplikowane. Istnieją trzy różne scenariusze usuwania, które musimy rozważyć.
Wszystkie liczby zostaną po prostu dodane do prawej gałęzi poprzedniej. Jeśli chcemy znaleźć liczbę, nie będziemy mieli innego wyjścia, jak po prostu podążać za łańcuchem w dół. 
Nie jest to lepsze niż wyszukiwanie liniowe. Istnieją inne struktury danych, które są bardziej złożone. Ale na razie nie będziemy ich rozważać. Powiedzmy, że aby rozwiązać problem konstruowania drzewa z posortowanej listy, możesz losowo mieszać dane wejściowe.
Główną ideą jest podzielenie naszej listy na dwie części, posortowaną i nieposortowaną. Na każdym etapie algorytmu nowa liczba jest przenoszona z części nieposortowanej do części posortowanej i tak dalej, aż wszystkie liczby znajdą się w części posortowanej.
Minimalną liczbę znajdujemy w nieposortowanej części tablicy (czyli na tym etapie – w całej tablicy). Ta liczba to 2. Teraz zamieniamy ją na pierwszą spośród nieposortowanych i umieszczamy ją na końcu posortowanej tablicy (w tym kroku - na pierwszym miejscu). W tym kroku jest to pierwsza liczba w tablicy, czyli 3. 
Krok drugi. Nie patrzymy na liczbę 2; znajduje się ona już w posortowanej podtablicy. Zaczynamy szukać minimum zaczynając od drugiego elementu, czyli 5. Dbamy o to, aby 3 było minimum wśród nieposortowanych, 5 było pierwszym wśród nieposortowanych. Zamieniamy je i dodajemy 3 do posortowanej podtablicy. 
W trzecim kroku widzimy, że najmniejszą liczbą w nieposortowanej tablicy jest 4. Zamieniamy ją na pierwszą liczbę spośród nieposortowanych - 5. 
W czwartym kroku stwierdzamy, że w nieposortowanej tablicy najmniejszą liczbą jest 5. Zmieniamy go z 6 i dodajemy do posortowanej podtablicy. 
Jeżeli wśród nieposortowanych (największych) pozostanie tylko jedna liczba, oznacza to, że cała tablica jest posortowana! 
Tak wygląda implementacja tablicy w kodzie. Spróbuj zrobić to sam. 
Zarówno w najlepszym, jak i najgorszym przypadku, aby znaleźć minimalny nieposortowany element, musimy porównać każdy element z każdym elementem nieposortowanej tablicy i będziemy to robić przy każdej iteracji. Ale nie musimy przeglądać całej listy, a jedynie nieposortowaną część. Czy zmienia to szybkość algorytmu? W pierwszym kroku dla tablicy składającej się z 5 elementów dokonujemy 4 porównań, w drugim - 3, w trzecim - 2. Aby otrzymać liczbę porównań należy wszystkie te liczby zsumować. Otrzymujemy sumę. 
Zatem oczekiwana prędkość algorytmu w najlepszym i najgorszym przypadku wynosi Θ(n 2 ). Nie jest to najbardziej wydajny algorytm! Jednak do celów edukacyjnych i dla małych zbiorów danych jest to całkiem przydatne.
Krok 1: przejdź przez tablicę. Algorytm zaczyna od dwóch pierwszych elementów, 8 i 6, i sprawdza, czy są one ułożone we właściwej kolejności. 8 > 6, więc zamieniamy je. Następnie patrzymy na drugi i trzeci element, teraz są to 8 i 4. Z tych samych powodów zamieniamy je. Po raz trzeci porównujemy 8 i 2. W sumie dokonujemy trzech wymian (8, 6), (8, 4), (8, 2). Wartość 8 „przepłynęła” na koniec listy we właściwym miejscu. 
Krok 2: zamień (6,4) i (6,2). Numer 6 znajduje się teraz na przedostatniej pozycji i nie ma potrzeby porównywać go z już posortowanym „ogonem” listy. 
Krok 3: zamień 4 i 2. Czwórka „unosi się” na swoje właściwe miejsce. 
Krok 4: przeglądamy tablicę, ale nie mamy już nic do zmiany. Oznacza to, że tablica jest całkowicie posortowana. 
A to jest kod algorytmu. Spróbuj zaimplementować to w C! Sortowanie bąbelkowe w najgorszym przypadku 
zajmuje O(n 2 ) czasu (wszystkie liczby są błędne), ponieważ w każdej iteracji musimy wykonać n kroków, których też jest n. Faktycznie, podobnie jak w przypadku algorytmu sortowania przez selekcję, czas będzie nieco krótszy (n 2 /2 – n/2), ale można to pominąć. W najlepszym przypadku (jeśli wszystkie elementy są już na swoim miejscu) możemy to zrobić w n krokach, tj. Ω(n), ponieważ będziemy musieli tylko raz wykonać iterację po tablicy i upewnić się, że wszystkie elementy są na swoich miejscach (tj. nawet elementy n-1).
Przyjrzyjmy się, jak działa sortowanie przez wstawianie, korzystając z poniższego przykładu. Zanim zaczniemy, wszystkie elementy uważa się za nieposortowane. 
Krok 1: Weź pierwszą nieposortowaną wartość (3) i wstaw ją do posortowanej podtablicy. Na tym etapie cała posortowana podtablica, jej początek i koniec będą wynosić właśnie te trzy. 
Krok 2: Ponieważ 3 > 5, wstawimy 5 do posortowanej podtablicy na prawo od 3. 
Krok 3: Teraz pracujemy nad wstawieniem liczby 2 do naszej posortowanej tablicy. Porównujemy 2 z wartościami od prawej do lewej, aby znaleźć właściwą pozycję. Ponieważ 2 < 5 i 2 < 3 i dotarliśmy do początku posortowanej podtablicy. Dlatego musimy wstawić 2 na lewo od 3. Aby to zrobić, przesuń 3 i 5 w prawo, aby było miejsce na 2 i wstaw je na początku tablicy. 
Krok 4. Mamy szczęście: 6 > 5, więc możemy wstawić tę liczbę zaraz po liczbie 5. 
Krok 5. 4 < 6 i 4 < 5, ale 4 > 3. Wiemy zatem, że do na prawo od 3. Ponownie jesteśmy zmuszeni przesunąć 5 i 6 w prawo, aby utworzyć lukę dla 4. 
Gotowe! Algorytm uogólniony: Weź każdy nieposortowany element n i porównaj go z wartościami w posortowanej podtablicy od prawej do lewej, aż znajdziemy odpowiednią pozycję dla n (to znaczy moment, w którym znajdziemy pierwszą liczbę mniejszą niż n) . Następnie przesuwamy wszystkie posortowane elementy znajdujące się na prawo od tej liczby w prawo, aby zrobić miejsce dla naszego n, i wstawiamy je tam, rozszerzając w ten sposób posortowaną część tablicy. Dla każdego nieposortowanego elementu n potrzebujesz:
Załóżmy, że mamy n elementów do posortowania. Jeśli n < 2, kończymy sortowanie, w przeciwnym razie sortujemy osobno lewą i prawą część tablicy, a następnie łączymy je. Posortujmy tablicę.Podzielmy 
ją na dwie części i kontynuujmy dzielenie, aż otrzymamy podtablice o rozmiarze 1, które są oczywiście posortowane. 
Dwie posortowane podtablice można połączyć w czasie O(n) za pomocą prostego algorytmu: usuń mniejszą liczbę z początku każdej podtablicy i wstaw ją do scalonej tablicy. Powtarzaj, aż znikną wszystkie elementy. 
Sortowanie przez scalanie zajmuje czas O(nlog n) dla wszystkich przypadków. Dzieląc tablice na połowy na każdym poziomie rekurencji, otrzymujemy log n. Następnie scalanie podtablic wymaga tylko n porównań. Zatem O(nlog n). Najlepsze i najgorsze przypadki sortowania przez scalanie są takie same, oczekiwany czas działania algorytmu = Θ(nlog n). Algorytm ten jest najskuteczniejszy spośród rozważanych. 
GO TO FULL VERSION