La clasificación es uno de los tipos básicos de actividades o acciones realizadas sobre objetos. Incluso en la infancia, a los niños se les enseña a clasificar, desarrollando su pensamiento. Las computadoras y los programas tampoco son una excepción. Existe una gran variedad de algoritmos. Te sugiero que mires qué son y cómo funcionan. Además, ¿qué pasa si un día te preguntan sobre uno de estos en una entrevista?
![Algoritmos de clasificación en teoría y práctica - 1]()
![Algoritmos de clasificación en teoría y práctica - 2]()
![Algoritmos de clasificación en teoría y práctica - 3]()
![Algoritmos de clasificación en teoría y práctica - 4]()
![Algoritmos de clasificación en teoría y práctica - 5]()
![Algoritmos de clasificación en teoría y práctica - 6]()
![Algoritmos de clasificación en teoría y práctica - 7]()
![Algoritmos de clasificación en teoría y práctica - 8]()
![Algoritmos de clasificación en teoría y práctica - 9]() Materiales:
Materiales:
![Algoritmos de clasificación en teoría y práctica - 10]()
L совпадёт с
Introducción
La clasificación de elementos es una de las categorías de algoritmos a las que un desarrollador debe acostumbrarse. Si alguna vez, cuando yo estudiaba, la informática no se tomaba tan en serio, ahora en la escuela deberían poder implementar algoritmos de clasificación y comprenderlos. Los algoritmos básicos, los más simples, se implementan mediante un buclefor. Naturalmente, para ordenar una colección de elementos, por ejemplo, una matriz, es necesario atravesar de alguna manera esta colección. Por ejemplo:
int[] array = {10, 2, 10, 3, 1, 2, 5};
for (int i = 0; i < array.length; i++) {
System.out.println(array[i]);
}int i) de 0 al último elemento de la matriz. Básicamente, simplemente tomamos cada elemento de la matriz e imprimimos su contenido. Cuantos más elementos haya en la matriz, más tardará en ejecutarse el código. Es decir, si n es el número de elementos, con n=10 el programa tardará 2 veces más en ejecutarse que con n=5. Cuando nuestro programa tiene un bucle, el tiempo de ejecución aumenta linealmente: cuantos más elementos, más larga será la ejecución. Resulta que el algoritmo del código anterior se ejecuta en tiempo lineal (n). En tales casos, se dice que la "complejidad del algoritmo" es O(n). Esta notación también se denomina "O grande" o "comportamiento asintótico". Pero simplemente puedes recordar "la complejidad del algoritmo".

La clasificación más sencilla (Bubble Sort)
Entonces, tenemos una matriz y podemos iterar sobre ella. Excelente. Intentemos ahora ordenarlo en orden ascendente. ¿Qué significa esto para nosotros? Esto significa que dados dos elementos (por ejemplo, a=6, b=5), debemos intercambiar a y b si a es mayor que b (si a > b). ¿Qué significa esto para nosotros cuando trabajamos con una colección por índice (como es el caso de una matriz)? Esto significa que si el elemento con índice a es mayor que el elemento con índice b, (matriz[a] > matriz[b]), dichos elementos deben intercambiarse. El cambio de lugar a menudo se denomina intercambio. Hay varias formas de cambiar de lugar. Pero utilizamos un código simple, claro y fácil de recordar:private void swap(int[] array, int ind1, int ind2) {
int tmp = array[ind1];
array[ind1] = array[ind2];
array[ind2] = tmp;
}int[] array = {10, 2, 10, 3, 1, 2, 5};
System.out.println(Arrays.toString(array));
for (int i = 1; i < array.length; i++) {
if (array[i] < array[i - 1]) {
swap(array, i, i-1);
}
}
System.out.println(Arrays.toString(array));int[] array = {10, 2, 10, 3, 1, 2, 5};
System.out.println(Arrays.toString(array));
boolean needIteration = true;
while (needIteration) {
needIteration = false;
for (int i = 1; i < array.length; i++) {
if (array[i] < array[i - 1]) {
swap(array, i, i-1);
needIteration = true;
}
}
}
System.out.println(Arrays.toString(array));while) hasta que decidimos que no se necesitan más iteraciones. De forma predeterminada, antes de cada nueva iteración, asumimos que nuestra matriz está ordenada y no queremos iterar más. Por lo tanto, repasamos los elementos secuencialmente y verificamos esta suposición. Pero si los elementos están desordenados, los intercambiamos y nos damos cuenta de que no estamos seguros de que ahora estén en el orden correcto. Por lo tanto, queremos realizar una iteración más. Por ejemplo, [3, 5, 2]. 5 son más que tres, todo está bien. Pero 2 es menor que 5. Sin embargo, [3, 2, 5] requiere una pasada más, porque 3 > 2 y es necesario intercambiarlos. Dado que utilizamos un bucle dentro de un bucle, resulta que la complejidad de nuestro algoritmo aumenta. Con n elementos se convierte en n * n, es decir O(n^2). Esta complejidad se llama cuadrática. Según tenemos entendido, no podemos saber exactamente cuántas iteraciones serán necesarias. El indicador de complejidad del algoritmo sirve para mostrar la tendencia al aumento de la complejidad, en el peor de los casos. ¿Cuánto aumentará el tiempo de ejecución cuando cambie el número de elementos n? La clasificación por burbujas es una de las más simples e ineficientes. A veces también se le llama "clasificación estúpida". Material relacionado:

Orden de selección
Otro tipo es el tipo de selección. También tiene complejidad cuadrática, pero hablaremos de eso más adelante. Entonces la idea es simple. Cada pasada selecciona el elemento más pequeño y lo mueve al principio. En este caso, comience cada nueva pasada moviéndose hacia la derecha, es decir, la primera pasada, desde el primer elemento, la segunda pasada, desde el segundo. Se verá así:int[] array = {10, 2, 10, 3, 1, 2, 5};
System.out.println(Arrays.toString(array));
for (int left = 0; left < array.length; left++) {
int minInd = left;
for (int i = left; i < array.length; i++) {
if (array[i] < array[minInd]) {
minInd = i;
}
}
swap(array, left, minInd);
}
System.out.println(Arrays.toString(array));- " JavaRush: Algoritmos de clasificación. Ordenación por selección "
- " CS50: Ordenación por selección "

Tipo de inserción
La ordenación por inserción también tiene complejidad cuadrática, ya que nuevamente tenemos un bucle dentro de otro bucle. ¿En qué se diferencia del tipo de selección? Esta clasificación es "estable". Esto significa que elementos idénticos no cambiarán su orden. Idéntico en cuanto a las características por las que clasificamos.int[] array = {10, 2, 10, 3, 1, 2, 5};
System.out.println(Arrays.toString(array));
for (int left = 0; left < array.length; left++) {
// Recuperar el valor del elemento
int value = array[left];
// Moverse a través de los elementos que están antes del elemento extraído
int i = left - 1;
for (; i >= 0; i--) {
// Si se extrae un valor más pequeño, mueva el elemento más grande más
if (value < array[i]) {
array[i + 1] = array[i];
} else {
// Si el elemento extraído es más grande, detener
break;
}
}
// Inserta el valor extraído en el espacio liberado
array[i + 1] = value;
}
System.out.println(Arrays.toString(array));- Ordenación por inserción de Java explicada
- CS50: Ordenación por inserción
- CS50 en JavaRush: ordenación por inserción

Ordenar lanzadera
Entre los tipos simples, hay otro: el tipo lanzadera. Pero prefiero la variedad lanzadera. Me parece que rara vez hablamos de transbordadores espaciales, y el transbordador es más bien una carrera. Por tanto, es más fácil imaginar cómo se lanzan los transbordadores al espacio. Aquí hay una asociación con este algoritmo. ¿Cuál es la esencia del algoritmo? La esencia del algoritmo es que iteramos de izquierda a derecha y, al intercambiar elementos, verificamos todos los demás elementos que quedan atrás para ver si es necesario repetir el intercambio.int[] array = {10, 2, 10, 3, 1, 2, 5};
System.out.println(Arrays.toString(array));
for (int i = 1; i < array.length; i++) {
if (array[i] < array[i - 1]) {
swap(array, i, i - 1);
for (int z = i - 1; (z - 1) >= 0; z--) {
if (array[z] < array[z - 1]) {
swap(array, z, z - 1);
} else {
break;
}
}
}
}
System.out.println(Arrays.toString(array));
Ordenar conchas
Otra clasificación simple es la clasificación Shell. Su esencia es similar a la clasificación de burbujas, pero en cada iteración tenemos una brecha diferente entre los elementos que se comparan. En cada iteración se reduce a la mitad. Aquí hay un ejemplo de implementación:int[] array = {10, 2, 10, 3, 1, 2, 5};
System.out.println(Arrays.toString(array));
// Calcular la brecha entre los elementos marcados
int gap = array.length / 2;
// Mientras haya una diferencia entre los elementos
while (gap >= 1) {
for (int right = 0; right < array.length; right++) {
// Mueva el puntero derecho hasta que podamos encontrar uno que
// no habrá suficiente espacio entre él y el elemento anterior
for (int c = right - gap; c >= 0; c -= gap) {
if (array[c] > array[c + gap]) {
swap(array, c, c + gap);
}
}
}
// Recalcular la brecha
gap = gap / 2;
}
System.out.println(Arrays.toString(array));- Ordenar conchas | Geeksparageeks
- Decisión AQA 1 2.03a Ordenación de conchas: un ejemplo con 8 números
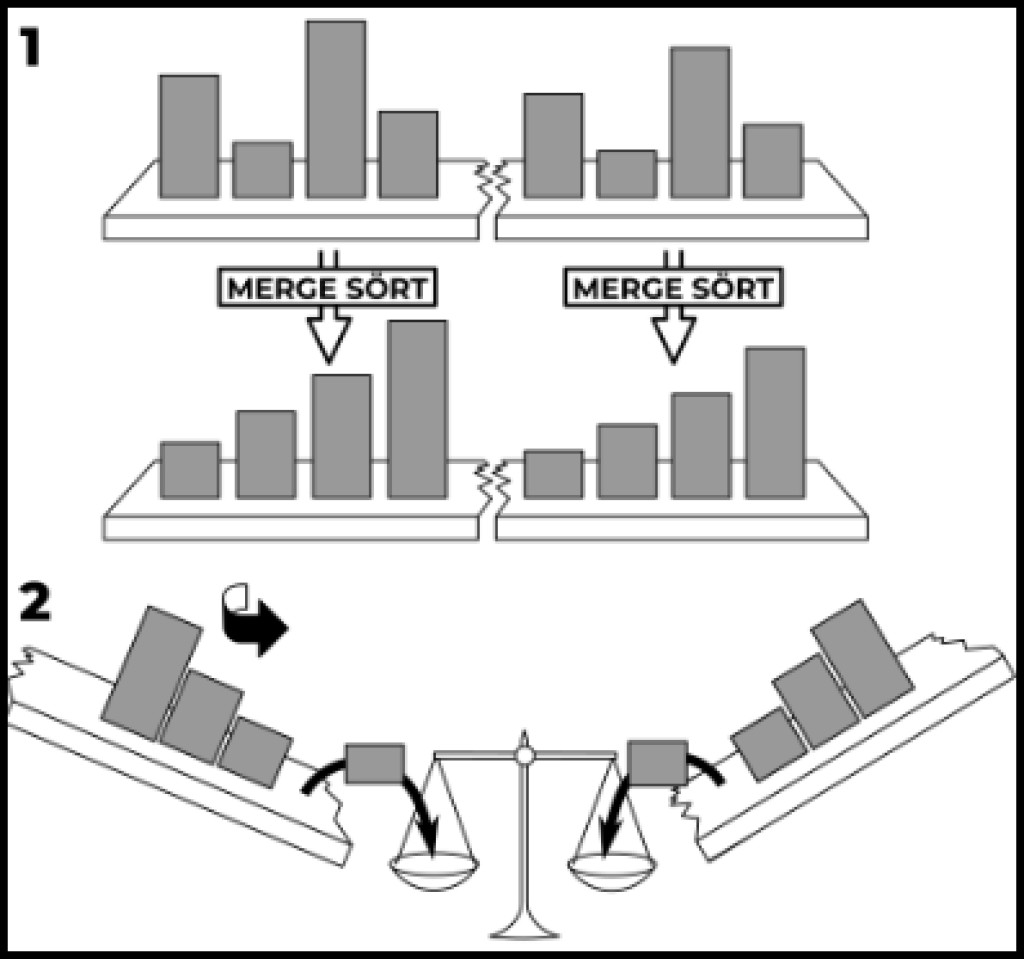
Combinar ordenar
Además de los tipos simples indicados, existen tipos más complejos. Por ejemplo, ordenar por combinación. En primer lugar, la recursividad vendrá en nuestra ayuda. En segundo lugar, nuestra complejidad ya no será cuadrática como estamos acostumbrados. La complejidad de este algoritmo es logarítmica. Escrito como O(n log n). Así que hagamos esto. Primero, escribamos una llamada recursiva al método de clasificación:public static void mergeSort(int[] source, int left, int right) {
// Elija un separador, es decir, dividir la matriz de entrada por la mitad
int delimiter = left + ((right - left) / 2) + 1;
// Ejecuta esta función recursivamente para las dos mitades (si podemos dividir (
if (delimiter > 0 && right > (left + 1)) {
mergeSort(source, left, delimiter - 1);
mergeSort(source, delimiter, right);
}
}public static void mergeSort(int[] source, int left, int right) {
// Elija un separador, es decir, dividir la matriz de entrada por la mitad
int delimiter = left + ((right - left) / 2) + 1;
// Ejecuta esta función recursivamente para las dos mitades (si podemos dividir (
if (delimiter > 0 && right > (left + 1)) {
mergeSort(source, left, delimiter - 1);
mergeSort(source, delimiter, right);
}
// Crea una matriz temporal con el tamaño deseado
int[] buffer = new int[right - left + 1];
// Comenzando desde el borde izquierdo especificado, recorre cada elemento
int cursor = left;
for (int i = 0; i < buffer.length; i++) {
// Usamos el delimitador para señalar el elemento del lado derecho
// Si delimitador > derecha, entonces no quedan elementos sin agregar en el lado derecho
if (delimiter > right || source[cursor] > source[delimiter]) {
buffer[i] = source[cursor];
cursor++;
} else {
buffer[i] = source[delimiter];
delimiter++;
}
}
System.arraycopy(buffer, 0, source, left, buffer.length);
}mergeSort(array, 0, array.length-1). Como puede ver, la esencia se reduce al hecho de que tomamos como entrada una matriz que indica el principio y el final de la sección a ordenar. Cuando comienza la clasificación, este es el principio y el final de la matriz. A continuación calculamos el delimitador: la posición del divisor. Si el divisor se puede dividir en 2 partes, entonces llamamos clasificación recursiva a las secciones en las que el divisor dividió la matriz. Preparamos una matriz de búfer adicional en la que seleccionamos la sección ordenada. A continuación, colocamos el cursor al inicio del área a ordenar y comenzamos a recorrer cada elemento del array vacío que hemos preparado y rellenarlo con los elementos más pequeños. Si el elemento señalado por el cursor es más pequeño que el elemento señalado por el divisor, colocamos este elemento en la matriz de búfer y movemos el cursor. De lo contrario, colocamos el elemento señalado por el separador en la matriz de búfer y movemos el separador. Tan pronto como el separador va más allá de los límites del área ordenada o llenamos toda la matriz, el rango especificado se considera ordenado. Material relacionado:

Ordenación por conteo y ordenación por base
Otro algoritmo de clasificación interesante es Counting Sort. La complejidad algorítmica en este caso será O(n+k), donde n es el número de elementos y k es el valor máximo del elemento. Hay un problema con el algoritmo: necesitamos conocer los valores mínimo y máximo de la matriz. A continuación se muestra un ejemplo de implementación de clasificación por conteo:public static int[] countingSort(int[] theArray, int maxValue) {
// Matriz con "contadores" que van desde 0 hasta el valor máximo
int numCounts[] = new int[maxValue + 1];
// En la celda correspondiente (índice = valor) aumentamos el contador
for (int num : theArray) {
numCounts[num]++;
}
// Preparar la matriz para el resultado ordenado
int[] sortedArray = new int[theArray.length];
int currentSortedIndex = 0;
// recorrer la matriz con "contadores"
for (int n = 0; n < numCounts.length; n++) {
int count = numCounts[n];
// ir por el número de valores
for (int k = 0; k < count; k++) {
sortedArray[currentSortedIndex] = n;
currentSortedIndex++;
}
}
return sortedArray;
}

Ordenación rápida de Java
Bueno, de postre, uno de los algoritmos más famosos: clasificación rápida. Tiene complejidad algorítmica, es decir, tenemos O(n log n). Este tipo también se llama tipo Hoare. Curiosamente, el algoritmo fue inventado por Hoare durante su estancia en la Unión Soviética, donde estudió traducción por computadora en la Universidad de Moscú y estaba desarrollando un libro de frases ruso-inglés. Este algoritmo también se utiliza en una implementación más compleja en Arrays.sort en Java. ¿Qué pasa con Collections.sort? Te sugiero que veas por ti mismo cómo se clasifican "debajo del capó". Entonces, el código:public static void quickSort(int[] source, int leftBorder, int rightBorder) {
int leftMarker = leftBorder;
int rightMarker = rightBorder;
int pivot = source[(leftMarker + rightMarker) / 2];
do {
// Mueve el marcador izquierdo de izquierda a derecha mientras el elemento es menor que el pivote
while (source[leftMarker] < pivot) {
leftMarker++;
}
// Mueve el marcador derecho hasta que el elemento sea mayor que el pivote
while (source[rightMarker] > pivot) {
rightMarker--;
}
// Comprueba si no necesitas intercambiar elementos señalados por marcadores
if (leftMarker <= rightMarker) {
// El marcador izquierdo solo será menor que el marcador derecho si tenemos que intercambiar
if (leftMarker < rightMarker) {
int tmp = source[leftMarker];
source[leftMarker] = source[rightMarker];
source[rightMarker] = tmp;
}
// Mover marcadores para obtener nuevos bordes
leftMarker++;
rightMarker--;
}
} while (leftMarker <= rightMarker);
// Ejecutar recursivamente para partes
if (leftMarker < rightBorder) {
quickSort(source, leftMarker, rightBorder);
}
if (leftBorder < rightMarker) {
quickSort(source, leftBorder, rightMarker);
}
}int[]fuente de la matriz de entrada, configuramos dos marcadores, izquierdo (L) y derecho (R). Cuando se llaman por primera vez, coinciden con el principio y el final de la matriz. A continuación, se determina el elemento de soporte, también conocido como pivot. Después de esto, nuestra tarea es mover los valores menores que pivota la izquierda pivoty los mayores a la derecha. Para ello, primero movemos el puntero Lhasta encontrar un valor mayor que pivot. Si no se encuentra un valor menor, entoncespivot. Потом двигаем указатель
R пока не найдём меньшее, чем
pivot significado. Если меньшее significado не нашли, то
R совпадёт с
pivot. Далее, если указатель
L находится до указателя
R o совпадает с ним, то пытаемся выполнить обмен элементов, если элемент
L меньше, чем
R. Далее
L сдвигаем вправо на 1 позицию,
R сдвигаем влево на одну позицию. Когда левый маркер
L окажется за правым маркером
R это будет означать, что обмен закончен, слева от
pivot меньшие значения, справа от
pivot — большие значения. После этого рекурсивно вызываем такую же сортировку для участков массива от начала сортируемого участка до правого маркера и от левого маркера до конца сортируемого участка. Почему от начала до правого? Потому что в конце итерации так и получится, что правый маркер сдвинется настолько, что станет границей части слева. Этот алгоритм более сложный, чем простая clasificación, поэтому его лучше зарисовать. Возьмём белый лист бумаги, запишем: 4 2 6 7 3 , а
Pivot по центру, т.е. число 6. Обведём его в круг. Под 4 напишем
L, под 3 напишем
R. 4 меньше чем 6, 2 меньше чем 6. Total,
L переместился на положение
pivot, т.к. по условию
L не может уйти дальше, чем
pivot. Напишем снова 4 2 6 7 3 , обведём 6 вкруг (
pivot) и поставим под ним
L. Теперь двигаем указатель
R. 3 меньше чем 6, поэтому ставим маркер
R на цифру 3. Так Cómo 3 меньше, чем
pivot 6 выполняем
swap, т.е. обмен. Запишем результат: 4 2 3 7 6 , обводим 6 вкруг, т.к. он по прежнему
pivot. Указатель
L на цифре 3, указатель
R на цифре 6. Мы помним, что двигаем указатели до тех пор, пока
L не зайдём за
R.
L двигаем на следующую цифру. Тут хочется разобрать два варианта: если бы предпоследняя цифра была 7 и если бы она была не 7, а 1.
Предпоследня цифра 1: Сдвинули указатель
L на цифру 1, т.к. мы можем двигать
L до тех пор, пока указатель
L указывает на цифру, меньшую чем
pivot. А вот
R мы не можем сдвинуть с 6, т.к. R не мы можем двигать только если указатель
R указывает на цифру, которая больше чем
pivot.
swap не делаем, т.к. 1 меньше 6. Записываем положение: 4 2 3 1 6, обводим
pivot 6.
L сдвигается на
pivot и больше не двигается.
R тоже не двигается. Обмен не производим. Сдвигаем
L и
R на одну позицию и подписываем цифру 1 маркером
R, а
L получается вне числа. Т.к.
L вне числа — ничего не делаем, а вот часть 4 2 3 1 выписываем снова, т.к. это наша левая часть, меньшая, чем
pivot 6. Выделяем новый
pivot и начинаем всё снова )
Предпоследняя цифра 7: Сдвинули указать
L на цифру 7, правый указатель не можем двигать, т.к. он уже указывает на pivot. т.к. 7 больше, чем
pivot, то делаем
swap. Запишем результат: 4 2 3 6 7, обводим 6 кружком, т.к. он
pivot. Указатель
L теперь сдвигается на цифру 7, а указатель
R сдвигается на цифру 3. Часть от
L до конца нет смысла сортировать, т.к. там всего 1 элемент, а вот часть от 4 до указателя
R отправляем на сортировку. Выбираем
pivot и начинаем всё снова ) Может на первый взгляд показаться, что если расставить много одинаковых с
pivot значений, это сломает алгоритм, но это не так. Можно напридумывать каверзных вариантов и на бумажке убедиться, что всё правильно и подивиться, Cómo такие простые действия предоставляют такой надёжный механизм. Единственный минус — такая clasificación не является стабильной. Т.к. при выполнении обмена одинаковые элементы могут поменять свой порядок, если один из них встретился до
pivot до того, Cómo другой элемент попал в часть до
pivot при помощи обмена. Материал:

GO TO FULL VERSION