Виміряти швидкість алгоритму реальним часом – секундами та хвабонами – непросто. Одна програма може працювати повільніше за іншу не через власну неефективність, а через повільність операційної системи, несумісність з обладнанням, зайнятість пам'яті комп'ютера іншими процесами… Щоб вимірювати ефективність алгоритмів, вигадали універсальні концепції незалежно від середовища, в якому запущено програму. Вимірювання асимптотичної складності задачі вимірюється за допомогою нотації О-великого. Нехай f(x) і g(x) — функції, визначені в околиці x0, причому g там не звертається в 0. Тоді f є «O» більшим від g при (x -> x0), якщо існує константа C>0 , Що всім x з деякої околиці точки x0 має місце нерівність |f(x)| <= C |g(x)| Трохи менш суворо: f є «O» більшим від g, якщо існує константа C>0, що всім x > x0 f(x) <= C*g(x) Не бійтеся формального визначення! По суті воно визначає асимптотичне зростання часу роботи програми, коли кількість ваших даних на вході зростає у бік нескінченності. Наприклад, ви порівнюєте сортування масиву з 1000 елементів та 10 елементів і потрібно зрозуміти, як зросте при цьому час роботи програми. Або потрібно підрахувати довжину рядка символів шляхом посимвольного проходу та додатком 1 за кожний символ: c - 1 a - 2 t - 3 Його асимптотична швидкість = О(n), де n – кількість літер у слові. Якщо вважати за таким принципом, час, необхідний підрахунку всього рядка, пропорційно кількості символів. Підрахунок кількості символів у рядку з 20 символів займає вдвічі більше часу, ніж підрахунку кількості символів у десятисимвольному рядку. Уявіть, що в змінній length ви зберегли значення, що дорівнює кількості символів у рядку. Наприклад, length = 1000. Щоб отримати довжину рядка, потрібен лише доступ до цієї змінної, на самий рядок можна навіть не дивитися. І як би ми не змінювали довжину, ми завжди можемо звернутися до цієї змінної. У такому разі асимптотична швидкість = O(1). Від зміни вхідних даних швидкість роботи у такому завданні не змінюється, пошук завершується за постійний час. У такому разі програма є асимптотично постійною. Недолік: ви витрачаєте пам'ять комп'ютера на збереження додаткової змінної та додатковий час оновлення її значення. Якщо вам здається, що лінійний час це погано, сміємо запевнити: буває набагато гірше. Наприклад, O(n 2 ). Такий запис означає, що зі зростанням n зростання часу, необхідного для перебору елементів (чи іншої дії) зростатиме все різкіше. Але за невеликих n алгоритми з асимптотической швидкістю О(n 2 ) можуть працювати швидше, ніж алгоритми з асимптотикою О(n). Але в якийсь момент квадратична функція обжене лінійну, від цього не втекти. Ще одна асимптотична складність – логарифмічний час або O(log n). Зі зростанням n ця функція зростає дуже повільно. О(log n) - час роботи класичного алгоритму бінарного пошуку у відсортованому масиві (пам'ятаєте розірваний телефонний довідник на лекції?). Масив ділиться надвоє, потім вибирається та половина, в якій знаходиться елемент і так щоразу зменшуючи область пошуку вдвічі, ми шукаємо елемент. Що буде, якщо ми відразу натрапимо на шукане, розділивши вперше наш масив даних навпіл? Для кращого часу є термін - омега-велике або Ω (n). У разі бінарного пошуку = Ω(1) (знаходить за постійний час незалежно від розміру масиву). Лінійний пошук працює за час O(n) і Ω(1), якщо елемент, що шукається, — найперший. Ще один символ – тета (Θ(n)). Він використовується, коли найкращий і найгірший варіанти однакові. Це підходить для прикладу, де ми зберігали довжину рядка в окремій змінній, тому за будь-якої її довжини достатньо звернутися до цієї змінної. Для цього алгоритму найкращий і найгірший варіанти рівні відповідно Ω(1) та O(1). Отже, алгоритм працює під час Θ(1).
Лінійний пошук
Коли ви відкриваєте веб-браузер, шукаєте сторінку, інформацію, друзів у соцмережах, ви здійснюєте пошук, так само, як при спробі знайти потрібну пару взуття в магазині. Ви, напевно, помічали, що впорядкованість сильно впливає на те, як ви шукаєте. Якщо у вас всі сорочки лежать у шафі, знайти серед них потрібну зазвичай простіше, ніж серед розкиданих без системи по всій кімнаті. Лінійний пошук - спосіб послідовного пошуку, один за одним. Коли ви переглядаєте результати пошуку в Google зверху вниз, ви використовуєте лінійний пошук. Приклад . нехай ми маємо список чисел: 2 4 0 5 3 7 8 1 І нам потрібно знайти 0. Ми його бачимо відразу, але комп'ютерна програма так не працює. Вона починає з початку списку та бачить число 2. Потім перевіряє, 2 = 0? Це не так, тому вона продовжує роботу та переходить до другого символу. Там на неї теж чекає невдача, і лише на третій позиції алгоритм знаходить потрібне число. Псевдокод лінійного пошуку: Функція linearSearch отримує на вхід два аргументи - ключ key і масив array []. Ключ - шукане значення, в попередньому прикладі key = 0. Масив - список чисел, які ми будемо переглядати. Якщо нічого не знайшли, функція поверне -1 (позицію, якої у масиві немає). Якщо ж лінійний пошук знайде потрібний елемент, то функція поверне позицію, де перебуває шуканий елемент у масиві. У лінійному пошуку добре те, що він працюватиме для будь-якого масиву, незалежно від порядку елементів: ми все одно пройдемо по всьому масиву. Це ж є його слабкістю. Якщо потрібно знайти число 198 в масиві з 200 чисел, відсортованих по порядку, цикл for пройде 198 кроків. Ви, мабуть, вже здогадалися, який спосіб працює краще для відсортованого масиву?
Бінарний пошук та дерева
Уявіть, що у вас є список відсортованих за алфавітом героїв діснеїв, і вам потрібно знайти Міккі Мауса. Лінійно це було б довго. А якщо скористатися «методом розриву довідника навпіл», ми потрапляємо відразу на Jasmine, і можемо сміливо відкинути першу половину списку, розуміючи, що Mickey там не може бути. За цим же принципом відкидаємо другий стовпець. Продовжуючи таку стратегію, ми знайдемо Міккі за пару кроків. Давайте знайдемо число 144. Ділимо список навпіл, і потрапляємо на число 13. Оцінюємо, більше чи менше шукане число, ніж 13. 13 < 144, так що ми можемо ігнорувати все, що знаходиться лівіше 13 і саме це число. Тепер наш список пошуку виглядає так: 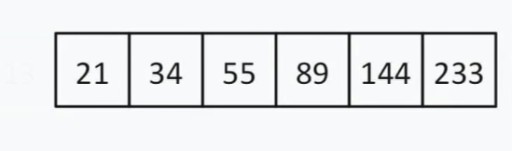Тут парна кількість елементів, тому вибираємо принцип, за яким вибираємо «середнє» (ближче до початку чи кінця). Допустимо, ми обрали стратегію близькості до початку. У такому разі наша «середина» = 55. 55 < 144. Ми знову відкидаємо ліву половину списку. На щастя для нас, наступне середнє число буде 144. Ми знайшли 144 в масиві з 13 елементів за допомогою бінарного пошуку всього за три кроки. Лінійний пошук у такій ситуації справився б аж за 12 кроків. Оскільки цей алгоритм на кожному кроці зменшує кількість елементів у масиві вдвічі, він знайде шуканий за асимптотичний час О(log n), де n – кількість елементів у списку. Тобто, у нашому випадку асимптотичний час = O(log 13) (це трохи більше трьох). Псевдокод функції бінарного пошуку: 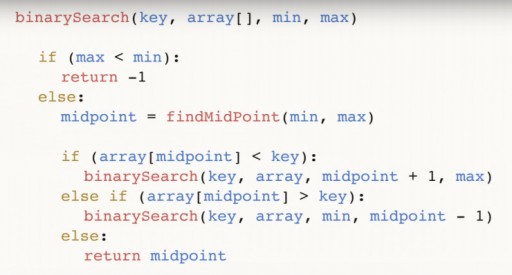Функція приймає на вхід 4 аргументи: шукане key, масив даних array [], в якому знаходиться шукане, min і max - покажчики на максимальне та мінімальне число в масиві, на яке ми дивимося на цьому кроці алгоритму. Для нашого прикладу спочатку дано таке зображення: Розберемо код далі. midpoint – наша середина масиву. Вона залежить від крайніх точок і знаходиться в центрі між ними. Після того, як ми знайшли середину, перевіряємо, чи вона менша від нашого числа key. Якщо це так, то key також більше, ніж будь-яке з чисел лівіше за середину, і ми можемо викликати бінарну функцію знову, тільки тепер наш min = midpoint + 1. Якщо виявиться, що key < midpoint, ми можемо відкинути саме це число і всі числа лежачи праворуч від нього. І ми викликаємо бінарний пошук масиву від числа min і аж до значення (midpoint – 1). Нарешті, третя гілка: якщо значення в середнійточці не більше і не менше, ніж key, йому нічого не залишається, як бути шуканим числом. Його ми й повертаємо у такому разі і закінчуємо роботу програми. Нарешті, може статися так, що число, яке шукається, і зовсім відсутнє в масиві. Для обліку цього випадку робимо таку перевірку: І повертаємо (-1), щоб зазначити, що ми нічого не знайшли. Ви знаєте, що для бінарного пошуку необхідно, щоб масив був відсортований. Таким чином, якщо у нас є невідсортований масив, в якому потрібно знайти якийсь елемент, ми маємо два варіанти дії:
Відсортувати список та застосувати бінарний пошук
Зберігати список завжди відсортованим при одночасному додаванні та видаленні з нього елементів.
Один із способів зберігання списків відсортованим вважається бінарне дерево пошуку. Бінарне (двійкове) дерево пошуку – це структура даних, яка відповідає таким вимогам:
Воно є деревом (структурою даних, що емулює деревоподібну структуру - має корінь та інші вузли (листя), пов'язані «гілками» або ребрами без циклів)
Кожен вузол має 0, 1 або 2 нащадки
Обидва піддерева - ліве та праве - є двійковими деревами пошуку.
У всіх вузлів лівого піддерева довільного вузла X значення ключів даних менше, ніж значення ключа даних самого вузла X.
У всіх вузлів правого поддерева довільного вузла X значення ключів даних більше чи одно, ніж значення ключа даних самого вузла X.
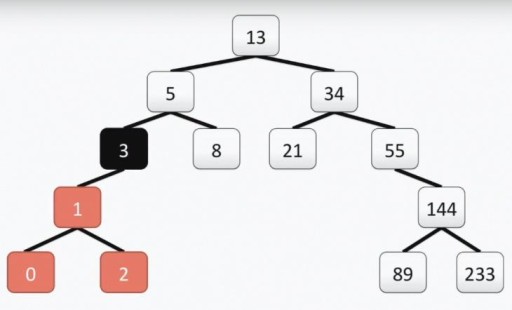Увага: корінь "програмістського" дерева, на відміну від реального, знаходиться зверху. Кожен осередок називається вершиною, вершини з'єднані ребрами. Корінь дерева — комірка з номером 13. Ліве піддерево вершини 3 виділено кольором на малюнку знизу: Наше дерево відповідає всім вимогам до бінарних дерев. Це означає, що кожне його ліве піддерево містить тільки значення, які менші або рівні значення вершини, праве - тільки значення великі або рівні значення вершини. Обидва ліві та праві піддерева самі є бінарними піддеревами. Спосіб побудови бінарного дерева - не єдиний: нижче на картинці ви бачите ще один варіант для того ж набору чисел, і їх може бути дуже багато на практиці. Така структура допомагає проводити пошук: мінімальне значення знаходимо, рухаючись від вершини вліво-вниз щоразу. 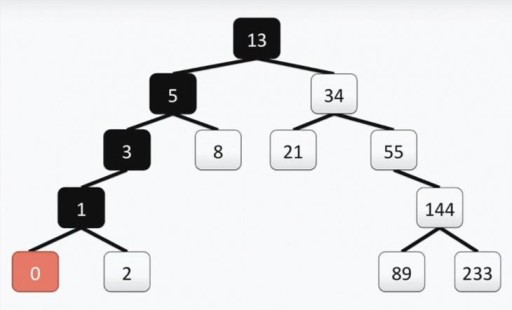Якщо потрібно знайти максимальну кількість - йдемо від вершини вниз і праворуч. Знаходження числа, яке не є мінімальним або максимальним, також дуже просте. Ми спускаємося від кореня вліво або вправо в залежності від того, більша чи менша наша вершина шукана. Так, якщо нам потрібно знайти число 89 ми проходимо такий шлях: Ще можна виводити числа в порядку сортування. Наприклад, якщо нам потрібно вивести всі числа в порядку зростання, беремо ліве піддерево і починаючи з лівої вершини йдемо нагору. Додати щось у дерево теж просто. Головне пам'ятати про структуру. Скажімо, нам потрібно додати до дерева значення 7. Ідемо до кореня, і перевіряємо. Число 7 < 13, тому йдемо вліво. Там бачимо 5, і йдемо вправо, оскільки 7 > 5. Далі оскільки 7 > 8 і 8 немає нащадків, ми конструюємо гілку від 8 вліво і її чіпляємо 7. Також можна видаляти вершини з дерева, але це трохи складніше. Є три різні сценарії для видалення, які ми повинні врахувати.
Найпростіший варіант: нам потрібно видалити вершину, яка не має нащадків. Наприклад, число 7, яке ми щойно додали. У такому разі ми просто проходимо шлях до вершини з цим числом та видаляємо його.
У вершини є одна вершина-нащадок. У разі можна видалити необхідну вершину, та її нащадка треба приєднати до «дідуся», тобто вершині, з якої виростав її безпосередній предок. Наприклад, з того ж дерева потрібно видалити число 3. У такому разі, її нащадка, одиницю, разом з усім піддеревом приєднуємо до 5. Це робиться просто, оскільки всі вершини, ліворуч від 5, будуть меншими за це число (і менше, ніж віддалена трійка).
Найскладніший випадок — коли у вершини, що видаляється, є два нащадки. Тепер перш за все нам потрібно знайти вершину, в якій заховано наступне більше значення, потрібно поміняти їх місцями, а потім видалити потрібну вершину. Зверніть увагу: вершина, що наступна за значенням, не може мати двох нащадків, тоді її лівий нащадок буде кращим кандидатом на наступне значення. Давайте з нашого дерева видалимо кореневу вершину 13. Спочатку шукаємо найближче до 13 число, яке його більше. Це 21. Змінюємо 21 та 13 місцями і видаляємо 13.
Є різні способи будувати бінарні дерева, одні добрі, інші не дуже. Що буде, якщо ми спробуємо збудувати бінарне дерево з відсортованого списку? Всі числа просто додаватимуться в праву гілку попереднього. Якщо ми захочемо знайти число, ми не матимемо іншого виходу, як просто йти по ланцюжку вниз. Це нітрохи не краще, ніж лінійний пошук. Є й інші структури даних, складніші. Але їх ми поки що розглядати не будемо. Скажімо, що для вирішення проблеми з побудовою дерева з відсортованого списку можна перемішати вхідні дані випадковим чином.
Алгоритми сортування
Є масив чисел. Потрібно його відсортувати. Для простоти вважатимемо, що ми сортуємо цілі числа в порядку зростання (від меншого до більшого). Існує кілька відомих способів провернути цей процес. Плюс, ви завжди можете пофантазувати на тему та придумати модифікацію алгоритму.
Сортування вибором
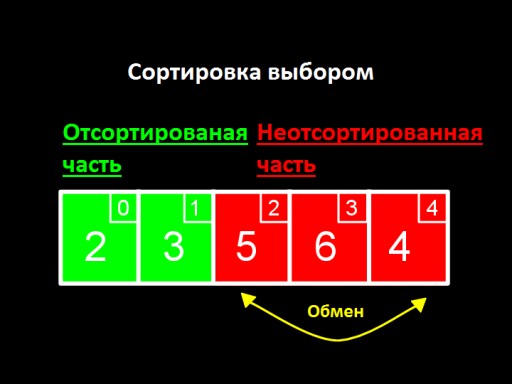Основна ідея – розбити наш список на дві частини, відсортовану та невідсортовану. На кожному кроці алгоритму нове число переміщається з невідсортованої частини у відсортовану, і так доки всі числа не виявляться у відсортованій частині.
Знаходимо мінімальне невідсортоване значення.
Змінюємо місцями це значення з першим невідсортованим значенням, ставлячи його таким чином наприкінці відсортованого масиву.
Якщо залишабося невідсортовані значення, повертаємось до кроку 1.
На першому кроці всі значення не відсортовані. Назвемо невідсортовану частину - Unsorted, а відсортовану - Sorted (це просто англійські слова, і робимо ми це тільки тому, що Sorted - набагато коротше, ніж "Відсортована частина" і краще виглядатиме на картинках). Знаходимо мінімальне число у невідсортованій частині масиву (тобто, на цьому кроці – у всьому масиві). Це число 2. Тепер змінюємо його з першим серед невідсортованих та ставимо його в кінець відсортованого масиву (на цьому кроці – на перше місце). На цьому етапі це перше число в масиві, тобто 3. Крок другий. На число 2 ми не дивимося, воно вже у відсортованому підмасиві. Починаємо шукати мінімальне, починаючи з другого елемента, це 5. Переконуємося, що 3 – мінімальне серед невідсортованих, 5 – перше серед невідсортованих. Змінюємо їх місцями і додаємо 3 до відсортованого підмасиву. На третьому кроці ми бачимо, що в невідсортованому підмасиві найменше число - 4. Змінюємо його з першим числом серед невідсортованих - 5. На четвертому кроці ми виявляємо, що в невідсортованому масиві мінімальне число - 5. Змінюємо його з 6 і додаємо до відсортованого подмасси . 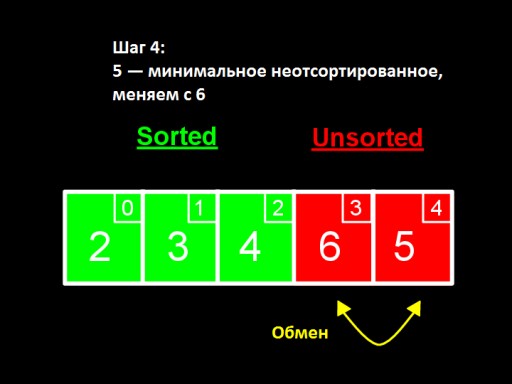Коли серед невідсортованих залишається лише одне число (найбільше), це означає, що масив відсортований! 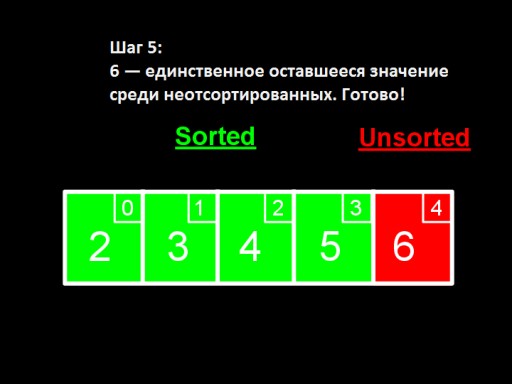Ось як виглядає реалізація масиву в коді. Спробуйте зробити її самостійно. В обох, найкращому та найгіршому випадку, щоб знайти мінімальний невідсортований елемент, ми повинні порівняти кожен елемент з кожним елементом невідсортованого масиву, і робити це ми будемо на кожній ітерації. Але нам потрібно переглядати не весь список, а лише невідсортовану частину. Чи змінює це швидкість алгоритму? На першому кроці для масиву з 5 елементів ми робимо 4 порівняння, на другому – 3, на третьому – 2. Щоб отримати кількість порівнянь, нам потрібно скласти усі ці числа. Ми отримуємо суму Таким чином, очікувана швидкість алгоритму в кращому і найгіршому випадку — Θ(n 2 ). Чи не найефективніший алгоритм! Тим не менш, для навчальних цілей і для невеликих масивів даних цілком застосовний.
Пухирцеве сортування
Алгоритм у бульбашкового сортування - один із найпростіших. Ідемо вздовж усього масиву і порівнюємо 2 сусідні елементи. Якщо вони у неправильному порядку, міняємо їх місцями. При першому проході наприкінці виявиться («спливе») найменший елемент (якщо ми сортуємо як спадання). Повторювати перший крок, якщо хоча б один обмін на попередньому кроці було здійснено. Давайте відсортуємо масив. Крок 1: йдемо масивом. Алгоритм починає роботу з перших двох елементів, 8 і 6 і перевіряє, чи вони в правильному порядку. 8 > 6, тому міняємо їх місцями. Далі ми дивимося на другий і третій елементи, тепер це 8 і 4. З тих самих міркувань міняємо їх місцями. Втретє порівнюємо 8 і 2. Отже, ми робимо три обміни (8, 6), (8, 4), (8, 2). Значення 8 "випливло" в кінець списку на правильну позицію. Крок 2: міняємо місцями (6,4) та (6,2). 6 тепер на передостанній позиції, і її можна не порівнювати з відсортованим «хвістом» списку. Крок 3: міняємо місцями 4 та 2. Четвірка «спливає» на своє законне місце. Крок 4: проходимося масивом, але міняти нам вже нічого. Це сигналізує у тому, що масив повністю відсортований. 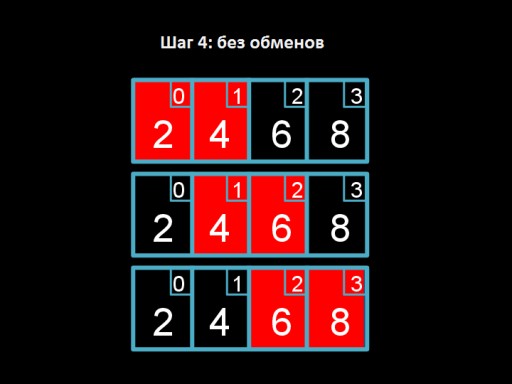А це код алгоритму. Спробуйте продати його на Сі! Бульбашкове сортування проходить за час O(n 2 ) у гіршому випадку (всі числа стоять неправильно), оскільки нам потрібно зробити n кроків на кожній ітерації, яких також n. Насправді, як і у випадку з алгоритмом сортування вибором, час буде дещо меншим (n 2 /2 – n/2), але цим можна знехтувати. У разі (якщо всі елементи вже стоять своєму місці), ми впораємося за n кроків, тобто. Ω(n), оскільки нам потрібно буде просто пробігтися масивом один раз і переконатися, що всі елементи стоять на своїх місцях (тобто навіть n-1 елементів).
Сортування вставками
Основна ідея цього алгоритму – поділ нашого масиву на дві частини, відсортовану та невідсортовану. На кожному кроці алгоритму число переходить від невідсортованого до відсортованої частини. Давайте на прикладі нижче розберемо, як працює сортування вставкою. До того як ми почали, всі елементи вважаються невідсортованими. Крок 1. Візьмемо перше невідсортоване значення (3) та вставимо його у відсортований підмасив. На цьому кроці весь відсортований підмасив, його початок і кінець і будуть цією трійкою. Крок 2. Оскільки 3 > 5, ми вставимо 5 у відсортований підмасив праворуч від 3. Крок 3. Тепер працюємо над вставкою числа 2 наш відсортований масив. Порівнюємо 2 зі значеннями праворуч наліво, щоб знайти правильну позицію. Оскільки 2 < 5 і 2 < 3 ми дійшли до початку відсортованого підмасиву. Отже, ми повинні вставити 2 зліва від 3. Для цього посуваємо 3 і 5 праворуч, щоб з'явилося місце для двійки і вставляємо її на початок масиву. Крок 4. Нам пощастило: 6 > 5, тому ми можемо вставити це число відразу за числом 5. Крок 5. 4 < 6 і 4 < 5, але 4 > 3. Отже ми знаємо, що 4 потрібно вставити праворуч від 3. Знову, ми змушені посунути 5 і 6 праворуч, щоб створити лакуну для 4. Готово! Узагальнений алгоритм: Беремо кожен невідсортований елемент n і порівнюємо його зі значеннями у відсортованому підмасиві справа наліво, поки не визначимо відповідну позицію для n (тобто, у той момент, коли знаходимо перше число, яке менше, ніж n). Потім зрушуємо всі відсортовані елементи, які знаходяться праворуч від цього числа праворуч, щоб утворилося місце для нашого n, м вставляємо його туди, тим самим розширюючи відсортовану частину масиву. Для кожного невідсортованого елемента потрібно:
Визначити місце у відсортованій частині масиву, куди потрібно вставити n
Зрушити відсортовані елементи вправо, щоб зробити лакуну для n
Вставити n в лакуну, що утворилася, у відсортованій частині масиву.
А ось і код! Рекомендуємо написати свою версію програми сортування.
Асимптотична швидкість алгоритму
У найгіршому випадку ми зробимо одне порівняння з другим елементом, два порівняння з третім тощо. Таким чином, наша швидкість дорівнює O(n 2 ). У кращому випадку ми працюватимемо з уже відсортованим масивом. Відсортована частина, яку ми будуємо зліва направо без вставок та пересувань елементів, займе час Ω(n).
Сортування злиттям
Цей алгоритм - рекурсивний, він розбиває одне велике завдання сортування на підзавдання, виконання яких роблять його ближчим до вирішення початкового великого завдання. Основна ідея – поділ невідсортованого масиву на дві частини та сортування окремих половинок за рекурсивним принципом. Допустимо, у нас є n елементів для сортування. Якщо n < 2, закінчуємо сортування, інакше сортуємо окремо ліву і праву частини масиву, і потім їх об'єднуємо. Давайте відсортуємо масив Ділимо його на дві частини, і продовжуємо ділити, поки не отримаємо підмасив величиною 1, які свідомо відсортовані. Два відсортованих підмасиву можна об'єднати за час O(n) за допомогою простого алгоритму: видаляємо менше числа на початку кожного підмасиву і вставляємо його в об'єднаний масив. Повторюємо, доки не закінчаться всі елементи. Сортування злиття вимагає часу O(nlog n) для всіх випадків. Поки що ми ділимо масиви на половини кожному рівні рекурсії отримуємо log n. Потім для злиття підмасивів потрібно всього n порівнянь. Отже, O(nlog n). Найкращий і найгірший варіанти для сортування злиттям - однакові, очікуваний час роботи алгоритму = Θ(nlog n). Цей алгоритм є найефективнішим серед розглянутих.
Але в якийсь момент квадратична функція обжене лінійну, від цього не втекти. Ще одна асимптотична складність – логарифмічний час або O(log n). Зі зростанням n ця функція зростає дуже повільно. О(log n) - час роботи класичного алгоритму бінарного пошуку у відсортованому масиві (пам'ятаєте розірваний телефонний довідник на лекції?). Масив ділиться надвоє, потім вибирається та половина, в якій знаходиться елемент і так щоразу зменшуючи область пошуку вдвічі, ми шукаємо елемент. 
Що буде, якщо ми відразу натрапимо на шукане, розділивши вперше наш масив даних навпіл? Для кращого часу є термін - омега-велике або Ω (n). У разі бінарного пошуку = Ω(1) (знаходить за постійний час незалежно від розміру масиву). Лінійний пошук працює за час O(n) і Ω(1), якщо елемент, що шукається, — найперший. Ще один символ – тета (Θ(n)). Він використовується, коли найкращий і найгірший варіанти однакові. Це підходить для прикладу, де ми зберігали довжину рядка в окремій змінній, тому за будь-якої її довжини достатньо звернутися до цієї змінної. Для цього алгоритму найкращий і найгірший варіанти рівні відповідно Ω(1) та O(1). Отже, алгоритм працює під час Θ(1).
Функція linearSearch отримує на вхід два аргументи - ключ key і масив array []. Ключ - шукане значення, в попередньому прикладі key = 0. Масив - список чисел, які ми будемо переглядати. Якщо нічого не знайшли, функція поверне -1 (позицію, якої у масиві немає). Якщо ж лінійний пошук знайде потрібний елемент, то функція поверне позицію, де перебуває шуканий елемент у масиві. У лінійному пошуку добре те, що він працюватиме для будь-якого масиву, незалежно від порядку елементів: ми все одно пройдемо по всьому масиву. Це ж є його слабкістю. Якщо потрібно знайти число 198 в масиві з 200 чисел, відсортованих по порядку, цикл for пройде 198 кроків. 
Ви, мабуть, вже здогадалися, який спосіб працює краще для відсортованого масиву?
Лінійно це було б довго. А якщо скористатися «методом розриву довідника навпіл», ми потрапляємо відразу на Jasmine, і можемо сміливо відкинути першу половину списку, розуміючи, що Mickey там не може бути. 
За цим же принципом відкидаємо другий стовпець. Продовжуючи таку стратегію, ми знайдемо Міккі за пару кроків. 
Давайте знайдемо число 144. Ділимо список навпіл, і потрапляємо на число 13. Оцінюємо, більше чи менше шукане число, ніж 13. 
13 < 144, так що ми можемо ігнорувати все, що знаходиться лівіше 13 і саме це число. Тепер наш список пошуку виглядає так: 
Тут парна кількість елементів, тому вибираємо принцип, за яким вибираємо «середнє» (ближче до початку чи кінця). Допустимо, ми обрали стратегію близькості до початку. У такому разі наша «середина» = 55. 
55 < 144. Ми знову відкидаємо ліву половину списку. На щастя для нас, наступне середнє число буде 144. 
Ми знайшли 144 в масиві з 13 елементів за допомогою бінарного пошуку всього за три кроки. Лінійний пошук у такій ситуації справився б аж за 12 кроків. Оскільки цей алгоритм на кожному кроці зменшує кількість елементів у масиві вдвічі, він знайде шуканий за асимптотичний час О(log n), де n – кількість елементів у списку. Тобто, у нашому випадку асимптотичний час = O(log 13) (це трохи більше трьох). Псевдокод функції бінарного пошуку: 
Функція приймає на вхід 4 аргументи: шукане key, масив даних array [], в якому знаходиться шукане, min і max - покажчики на максимальне та мінімальне число в масиві, на яке ми дивимося на цьому кроці алгоритму. Для нашого прикладу спочатку дано таке зображення: 
Розберемо код далі. midpoint – наша середина масиву. Вона залежить від крайніх точок і знаходиться в центрі між ними. Після того, як ми знайшли середину, перевіряємо, чи вона менша від нашого числа key. 
Якщо це так, то key також більше, ніж будь-яке з чисел лівіше за середину, і ми можемо викликати бінарну функцію знову, тільки тепер наш min = midpoint + 1. Якщо виявиться, що key < midpoint, ми можемо відкинути саме це число і всі числа лежачи праворуч від нього. І ми викликаємо бінарний пошук масиву від числа min і аж до значення (midpoint – 1). 
Нарешті, третя гілка: якщо значення в середнійточці не більше і не менше, ніж key, йому нічого не залишається, як бути шуканим числом. Його ми й повертаємо у такому разі і закінчуємо роботу програми. 
Нарешті, може статися так, що число, яке шукається, і зовсім відсутнє в масиві. Для обліку цього випадку робимо таку перевірку: 
І повертаємо (-1), щоб зазначити, що ми нічого не знайшли. Ви знаєте, що для бінарного пошуку необхідно, щоб масив був відсортований. Таким чином, якщо у нас є невідсортований масив, в якому потрібно знайти якийсь елемент, ми маємо два варіанти дії:
Увага: корінь "програмістського" дерева, на відміну від реального, знаходиться зверху. Кожен осередок називається вершиною, вершини з'єднані ребрами. Корінь дерева — комірка з номером 13. Ліве піддерево вершини 3 виділено кольором на малюнку знизу: 
Наше дерево відповідає всім вимогам до бінарних дерев. Це означає, що кожне його ліве піддерево містить тільки значення, які менші або рівні значення вершини, праве - тільки значення великі або рівні значення вершини. Обидва ліві та праві піддерева самі є бінарними піддеревами. Спосіб побудови бінарного дерева - не єдиний: нижче на картинці ви бачите ще один варіант для того ж набору чисел, і їх може бути дуже багато на практиці. 
Така структура допомагає проводити пошук: мінімальне значення знаходимо, рухаючись від вершини вліво-вниз щоразу. 
Якщо потрібно знайти максимальну кількість - йдемо від вершини вниз і праворуч. Знаходження числа, яке не є мінімальним або максимальним, також дуже просте. Ми спускаємося від кореня вліво або вправо в залежності від того, більша чи менша наша вершина шукана. Так, якщо нам потрібно знайти число 89 ми проходимо такий шлях: 
Ще можна виводити числа в порядку сортування. Наприклад, якщо нам потрібно вивести всі числа в порядку зростання, беремо ліве піддерево і починаючи з лівої вершини йдемо нагору. Додати щось у дерево теж просто. Головне пам'ятати про структуру. Скажімо, нам потрібно додати до дерева значення 7. Ідемо до кореня, і перевіряємо. Число 7 < 13, тому йдемо вліво. Там бачимо 5, і йдемо вправо, оскільки 7 > 5. Далі оскільки 7 > 8 і 8 немає нащадків, ми конструюємо гілку від 8 вліво і її чіпляємо 7. Також можна видаляти 
вершини з дерева, але це трохи складніше. Є три різні сценарії для видалення, які ми повинні врахувати.
Всі числа просто додаватимуться в праву гілку попереднього. Якщо ми захочемо знайти число, ми не матимемо іншого виходу, як просто йти по ланцюжку вниз. 
Це нітрохи не краще, ніж лінійний пошук. Є й інші структури даних, складніші. Але їх ми поки що розглядати не будемо. Скажімо, що для вирішення проблеми з побудовою дерева з відсортованого списку можна перемішати вхідні дані випадковим чином.
Основна ідея – розбити наш список на дві частини, відсортовану та невідсортовану. На кожному кроці алгоритму нове число переміщається з невідсортованої частини у відсортовану, і так доки всі числа не виявляться у відсортованій частині.
Знаходимо мінімальне число у невідсортованій частині масиву (тобто, на цьому кроці – у всьому масиві). Це число 2. Тепер змінюємо його з першим серед невідсортованих та ставимо його в кінець відсортованого масиву (на цьому кроці – на перше місце). На цьому етапі це перше число в масиві, тобто 3. 
Крок другий. На число 2 ми не дивимося, воно вже у відсортованому підмасиві. Починаємо шукати мінімальне, починаючи з другого елемента, це 5. Переконуємося, що 3 – мінімальне серед невідсортованих, 5 – перше серед невідсортованих. Змінюємо їх місцями і додаємо 3 до відсортованого підмасиву. 
На третьому кроці ми бачимо, що в невідсортованому підмасиві найменше число - 4. Змінюємо його з першим числом серед невідсортованих - 5. На четвертому кроці ми виявляємо, 
що в невідсортованому масиві мінімальне число - 5. Змінюємо його з 6 і додаємо до відсортованого подмасси . 
Коли серед невідсортованих залишається лише одне число (найбільше), це означає, що масив відсортований! 
Ось як виглядає реалізація масиву в коді. Спробуйте зробити її самостійно. 
В обох, найкращому та найгіршому випадку, щоб знайти мінімальний невідсортований елемент, ми повинні порівняти кожен елемент з кожним елементом невідсортованого масиву, і робити це ми будемо на кожній ітерації. Але нам потрібно переглядати не весь список, а лише невідсортовану частину. Чи змінює це швидкість алгоритму? На першому кроці для масиву з 5 елементів ми робимо 4 порівняння, на другому – 3, на третьому – 2. Щоб отримати кількість порівнянь, нам потрібно скласти усі ці числа. Ми отримуємо суму 
Таким чином, очікувана швидкість алгоритму в кращому і найгіршому випадку — Θ(n 2 ). Чи не найефективніший алгоритм! Тим не менш, для навчальних цілей і для невеликих масивів даних цілком застосовний.
Крок 1: йдемо масивом. Алгоритм починає роботу з перших двох елементів, 8 і 6 і перевіряє, чи вони в правильному порядку. 8 > 6, тому міняємо їх місцями. Далі ми дивимося на другий і третій елементи, тепер це 8 і 4. З тих самих міркувань міняємо їх місцями. Втретє порівнюємо 8 і 2. Отже, ми робимо три обміни (8, 6), (8, 4), (8, 2). Значення 8 "випливло" в кінець списку на правильну позицію. 
Крок 2: міняємо місцями (6,4) та (6,2). 6 тепер на передостанній позиції, і її можна не порівнювати з відсортованим «хвістом» списку. 
Крок 3: міняємо місцями 4 та 2. Четвірка «спливає» на своє законне місце. 
Крок 4: проходимося масивом, але міняти нам вже нічого. Це сигналізує у тому, що масив повністю відсортований. 
А це код алгоритму. Спробуйте продати його на Сі! 
Бульбашкове сортування проходить за час O(n 2 ) у гіршому випадку (всі числа стоять неправильно), оскільки нам потрібно зробити n кроків на кожній ітерації, яких також n. Насправді, як і у випадку з алгоритмом сортування вибором, час буде дещо меншим (n 2 /2 – n/2), але цим можна знехтувати. У разі (якщо всі елементи вже стоять своєму місці), ми впораємося за n кроків, тобто. Ω(n), оскільки нам потрібно буде просто пробігтися масивом один раз і переконатися, що всі елементи стоять на своїх місцях (тобто навіть n-1 елементів).
Давайте на прикладі нижче розберемо, як працює сортування вставкою. До того як ми почали, всі елементи вважаються невідсортованими. 
Крок 1. Візьмемо перше невідсортоване значення (3) та вставимо його у відсортований підмасив. На цьому кроці весь відсортований підмасив, його початок і кінець і будуть цією трійкою. 
Крок 2. Оскільки 3 > 5, ми вставимо 5 у відсортований підмасив праворуч від 3. 
Крок 3. Тепер працюємо над вставкою числа 2 наш відсортований масив. Порівнюємо 2 зі значеннями праворуч наліво, щоб знайти правильну позицію. Оскільки 2 < 5 і 2 < 3 ми дійшли до початку відсортованого підмасиву. Отже, ми повинні вставити 2 зліва від 3. Для цього посуваємо 3 і 5 праворуч, щоб з'явилося місце для двійки і вставляємо її на початок масиву. 
Крок 4. Нам пощастило: 6 > 5, тому ми можемо вставити це число відразу за числом 5. 
Крок 5. 4 < 6 і 4 < 5, але 4 > 3. Отже ми знаємо, що 4 потрібно вставити праворуч від 3. Знову, ми змушені посунути 5 і 6 праворуч, щоб створити лакуну для 4. 
Готово! Узагальнений алгоритм: Беремо кожен невідсортований елемент n і порівнюємо його зі значеннями у відсортованому підмасиві справа наліво, поки не визначимо відповідну позицію для n (тобто, у той момент, коли знаходимо перше число, яке менше, ніж n). Потім зрушуємо всі відсортовані елементи, які знаходяться праворуч від цього числа праворуч, щоб утворилося місце для нашого n, м вставляємо його туди, тим самим розширюючи відсортовану частину масиву. Для кожного невідсортованого елемента потрібно:
Допустимо, у нас є n елементів для сортування. Якщо n < 2, закінчуємо сортування, інакше сортуємо окремо ліву і праву частини масиву, і потім їх об'єднуємо. Давайте відсортуємо масив 
Ділимо його на дві частини, і продовжуємо ділити, поки не отримаємо підмасив величиною 1, які свідомо відсортовані. 
Два відсортованих підмасиву можна об'єднати за час O(n) за допомогою простого алгоритму: видаляємо менше числа на початку кожного підмасиву і вставляємо його в об'єднаний масив. Повторюємо, доки не закінчаться всі елементи. 
Сортування злиття вимагає часу O(nlog n) для всіх випадків. Поки що ми ділимо масиви на половини кожному рівні рекурсії отримуємо log n. Потім для злиття підмасивів потрібно всього n порівнянь. Отже, O(nlog n). Найкращий і найгірший варіанти для сортування злиттям - однакові, очікуваний час роботи алгоритму = Θ(nlog n). Цей алгоритм є найефективнішим серед розглянутих. 
ПЕРЕЙДІТЬ В ПОВНУ ВЕРСІЮ